Home   ·   About   ·   Tipi   ·   Yurt / Ger   ·   Dome   ·   Features   ·   Gallery About Overview License Tipi Overview Tipi Diary Yurt / Ger Overview Yurt Notes & Calculator Yurt / Ger Diary Yurt Builder Conference Living Notes Material Notes Dome Overview Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Features Overview Chris Aeppli Claudius Kern René K. Müller Geodesic Solitude Johnny's Capsule Geodesic Clay Mud Dome Jurtendorf (Switzerland) Neolithics of Pfyn Strawbale Cabin Home Nomadic Shelters Considerations & Ratings Selecting & Preparing the Site Snow Slide on Roofs Clustering Attached Room Volume vs Surface Volume vs Floor Volume vs Roof What Form To Use? Aftermath Working with Models Site Search Enter term & press ENTER If you found the information useful, consider to make a donation:   Page << Prev | 1 | 2 | 3 | 4 | 5 | Next >> Volume vs Surface The main aim of a shelter is to create a roof to let rain flow aside and keep the ground beneath dry walls to protect from wind and cold with it, e.g. to keep a fire burning additional thicker walls to protect from cold, e.g. to keep heat from a fire more lasting as a result of one or more requirements, we end up with circumscribing a given volume, we create a solid. Usually we take material found in the environment to build a shelter, e.g. tree branches with leafs (see also Building Typology). One of the most simple construction is the one of a cone or tipi-like. In order to study various forms, let's look how good such a space can be circumscribed, the volume we assume given - how about the surface, and what part is exposed vertical as roof? For now I look for the dome, yurt, tipi and cube, and list first the calculations: A = surface area, Awall = surface area without ground area, Aroof = surface area weather exposed, V = volume Sphere A = 4 π r2 Aroof = 4 π r2 / 2 V = 4/3 π r3 Dome A = 4 π r2 / 2 + r2 π = 3 π r2 Awall = 4 π r2 / 2 = 2 π r2 Aroof = 4 π r2 / 2 = 2 π r2 V = 4/6 π r3 Cube A = 6 s2 Awall = 5 s2 Aroof = s2 V = s3 Cone / Tipi The tipi diameter is also the length s of the cone, therefore 2r = d = s; and h = √((2r)2-r2) = r √3 A = r2 π + r 2r &pi = 3 r2 π Awall = Aroof = 2 r2 π Afloor = r2 π V = 1/3 r2 π h = 1/3 r2 π √((2r)2-r2) = 1/3 r3 π √3 Yurt Following assumptions were made: 1/3 height is the roof, which has α angle, 2/3 height is the vertical wall. A = 2 r π (tan(α) r 2) + r π (r2+(tan(α) r)2)1/2 + r2 π =    r2π (4 tan(α) + (1+tan(α)2)1/2 + 1) Awall = 2 r π (tan(α) r 2) + r π (r2+(tan(α) r)2)1/2 =    r2 π (4 tan(α) + (1+tan(α)2)1/2 Aroof = r π (r2+(tan(α) r)2)1/2 =    r2 π (1+tan(α)2)1/2 V = r2 π (tan(α) r 2) + r2 π (tan(α) r / 3) = r3 π 7/3 tan(α) So, to have V set to 1m3 (and 25° roof angle for the yurt) and calculating all surfaces A via r or s: Asphere = 4 π ((1/(4/3 &pi))1/3)2 = 4.835 Adome = 3 π ((1/(4/6 &pi))1/3)2 = 5.757 Adome-wall = 2 π ((1/(4/6 &pi))1/3)2 = 3.838 Ayurt = (1/(π 7/3 tan(25°))1/3)2 (4 tan(25°) + (1+tan(25°)2)1/2 + 1) = 5.494 Ayurt-wall = (1/(π 7/3 tan(25°))1/3)2 (4 tan(25°) + (1+tan(25°)2)1/2) = 4.109 Acube = 6 (11/3)2 = 6 Acube-wall = 5 (11/3)2 = 5 Atipi = 3 π ((3/(π √3))1/3)2 6.337 Atipi-wall = 2 π ((3/(π √3))1/3)2 4.225 Now we can list the ratios: Asphere : Acube = 4.835 : 6 = 100% : 124.1% 85.6% : 100% Adome : Ayurt : Atipi : Acube = 5.757 : 5.494 : 6.337 : 6 = 100% : 95.4% : 110.1% : 104.2% 96.0% : 91.6% : 105.6% : 100% Adome-wall : Ayurt-wall : Atipi-wall : Acube-wall = 3.838 : 4.109 : 4.225 : 5 = 100% : 107.1% : 110.1% : 130.3% 76.6% : 82.1% : 84.5% : 100% Volume vs Surface (without ground area) 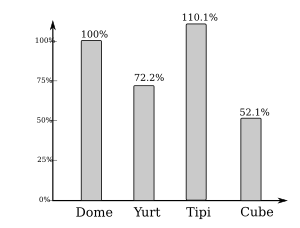The required heating is mainly dependent on the surface and secondary on the volume, and since we calculated anyway with the same volume, we focus on the surface, which requires thermal insulation in order to maintain the heat energy within the room. So, the lesser the surface circumventing a volume, the better, the lesser insulations is required, and lesser surface where the energy is able to be transfered. So, since I quickly led out the ratios, we can directly say, considering just the walls (without floor area), the dome requires 25-30% less energy and insulation than a cube given the same volume, and still have more ground area: Volume vs Floor Dome (V = 1m3) r = (1/(4/6 π))1/3 = 0.781 Afloor = r2 π = 1.919 100% Yurt (V = 1m3) r = (1/(π 7/3 tan(25°))1/3 = 0.664 Afloor = r2 π = 1.385 72.2% Tipi (V = 1m3) r = (3/(π √3))1/3 = 0.820 Afloor = r2 π = 2.112 110.1% Cube (V = 1m3) s = 11/3 = 1 Afloor = s2 = 1 52.1% 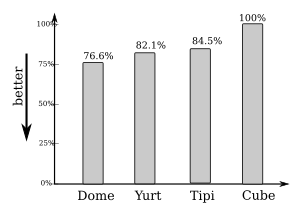Volume vs Floor In other words, given the same volume, saving 25-30% of wall insulation, and having almost twice the ground area. Since you get twice the ground area, when considering the ground area also as insulation area, the advantage shrinks to 4% solely. The yurt is alike the dome, 7% more surface than the dome (just the walls/roof), this is very good. The tipi, due it's form to extend toward the ground, gives most floor area for a given volume. I personally have a preference to consider larger floor area the better, as it's one of my aims. Yet, one may argue, as said, the grander floor requires more thermal insulation too. 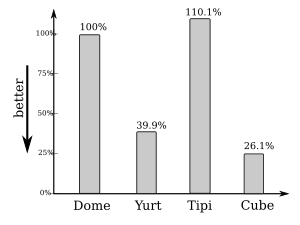Volume vs Roof Now, given the insights of the previous calculations, why aren't we building spherical? The answer will be given in this consideration: Dome (V = 1m3) r = (1/(4/6 π))1/3 = 0.781 Aroof = 2 r2 π = 3.838 100.0% 383.8% Yurt (V = 1m3) r = (1/(π 7/3 tan(25°))1/3 = 0.664 Aroof = r2 π (1 + tan(α)2)1/2 = 1.528 39.8% 152.8% Tipi (V = 1m3) r = (3/(π √3))1/3 = 0.820 Aroof = 2 r2 π = 4.224 110.1% 422.4% Cube (V = 1m3) s = 11/3 = 1 Aroof = s2 = 1 26.1% 100.0% Volume vs Roof The dome and tipi require 4x more material to be act as roof and be sealed 100% from water/rain than the roof of a cube. The yurt has apprx. 50% more roof surface than the cube, which is not that bad, given the yurt roof already is tilted, and the cube roof is not and the surface would increase as well if we had it tilted, e.g. 25° too. Lloyd Khan wrote in some of his critics about polyhedral domes (e.g. such as geodesic dome) that in case of domes the entire surface is a roof, unlike with an ordinary house which has a roof and wall, and a wall requires less water resistance than a roof. This is one of the main building disadvantages, which I think is also responsible why so few domes are built compared to rectangular/cubic houses with roofs; yet in case of temporary building the same argument applies of course. The yurt can be considered a compromise between circle/spherical and rectangular/cubic building, the ground floor is circular, yet has wall (no vertical exposure) and roof (vertical exposure). What Form To Use? The Volume vs Surface reveals the spherical construction does best, and this influences effectiveness of heating as its primarly depended on surface. But then the Volume vs Roof reveals the major drawback on spherical building, the former advantage of gaining due less material to use to enclose a given volume is vanished, by having almost 4x more vertical exposure, a roof which needs to seal rain completely. Now, what to do with these two considerations? If you live in a region with less rainfall, and do not need to pay so close attention to have a 100% waterproof roof, spherical or dome-wise is your choice - also if you live in a region where it's cold and you need to invest much into thermal insulation, but you have little to no rainfall. This leaves the rest, regions with significant rainfall, where a roof is required which indeed provides 100% seal of rain - and here cubic building does best, with a tilted roof of course so the rain flows on the side(s). The yurt, like said, a mixture of spherical and cubic building, provides a compromise - does well Volume vs Surface and Volume vs Roof. Why I am calculating this all - well first of all for myself as I was really curious what's the advantage truly, in numbers, not just knowing the sphere is the optimum of surface and volume but to see how a dome (half a sphere) relates to a cube or a yurt. Now we pretty much have a good overview. Aftermath I have been fascinated by geometrical forms yet some of them were too abstract and really until I started to work in real world with some of the forms it got me so to speak, especially when you build and live in them yourself. At such a point you actually immediatly experience a form, and especially since we are so used to cubic or rectangular rooms it is a new experience for the senses and spirit to live in spherical or circular rooms. We are dealing here with the archetypes of forms as such, and the circle, the square, the sphere, the cube and so forth, they are archetypes which connect us to the realm of abstract forms from where we develop, plan and finally build not just temporary buildings, but everything which finally has a physical form here. Next Page >> Page << Prev | 1 | 2 | 3 | 4 | 5 | Next >> Content: Page 1: Nomadic Shelters, Building Typology, Selected Shelters, Considerations & Ratings, Simplicity ... Page 2: Selecting & Preparing the Site, Unique Site Characteristics, Snow Slide on Roofs Page 3: Clustering, Tunnel with Door, Tunnel without Door, Without Tunnel, Heat Distribution in Clusters ... Page 4: Volume vs Surface, Volume vs Floor, Volume vs Roof, What Form To Use?, Aftermath Page 5: Working with Models Home   ·   About   ·   Tipi   ·   Yurt   ·   Dome   ·   Features   ·   Gallery Print   ·   Bookmark Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source