Home   ·   About   ·   Tipi   ·   Yurt / Ger   ·   Dome   ·   Features   ·   Gallery About Overview License Tipi Overview Tipi Diary Yurt / Ger Overview Yurt Notes & Calculator Yurt / Ger Diary Yurt Builder Conference Living Notes Material Notes Dome Overview Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Features Overview Chris Aeppli Claudius Kern René K. Müller Geodesic Solitude Johnny's Capsule Geodesic Clay Mud Dome Jurtendorf (Switzerland) Neolithics of Pfyn Strawbale Cabin Dome Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Introduction Geodesic Tetrahedron Geodesic Truncated Tetrahedron Geodesic Octahedron Geodesic Cube Geodesic Cuboctahedron Geodesic Truncated Octahedron Geodesic Truncated Cube Geodesic Rhombicuboctahedron Geodesic Truncated Cuboctahedron Geodesic Snub Cube Geodesic Icosahedron Geodesic Dodecahedron Geodesic Icosidodecahedron Geodesic Truncated Icosahedron Geodesic Truncated Dodecahedron Geodesic Rhombicosidodecahedron Geodesic Truncated Icosidodecahedron Geodesic Snub Dodecahedron Geodesic Pentakis Dodecahedron Other Solids Links Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Site Search Enter term & press ENTER If you found the information useful, consider to make a donation:   Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Geodesic Polyhedra written by Rene K. Mueller, Copyright (c) 2007, last updated Fri, February 25, 2022 Updates Wed, June 6, 2007: Added Pentakis Dodecahedron, with its famous 8V version of Epcot's "Spaceship Earth" sphere. . Wed, April 4, 2007: Added triacon variants and where suitable also the triacon dome variant as well . Sun, March 25, 2007: Redefined and clarified L0, L1, L2 and so forth, and better explanation of Ln vs nV . Mon, March 12, 2007: More details for each variant, incl. calculator for dome options. . Thu, March 1, 2007: Included dome variants when suitable, including strut maps. . Sun, February 25, 2007: First version with overview of platonic & archimedean geodesic forms, for now only L1 and L2 as I call them. . 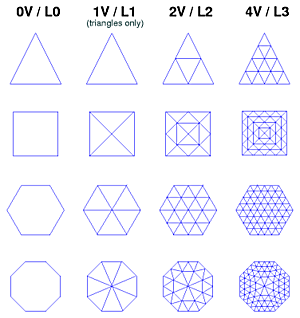Introduction After studying the geodesic dome (often direct associated to Buckminster Fuller but he wasn't the first), which essentially is derived from a Icosahedron, I thought to check the possibility to triangulate other platonic and archimedean solids. Based on the information I gathered from regular & semi-regular polyhedra I made this overview. Geodesic Procedure Triangle Divisions (Class 1/Alternate) Normalizing to Sphere The L0 is the original solid or face (n-sided), the L1 I created by centerpoint triangulation of the larger polygons (4, 5, 6, 8 or 10 sided polygons) until there are only triangles and normalized, the L2 is then the triangulated (class 1 or alternate method) & normalized version of L1. 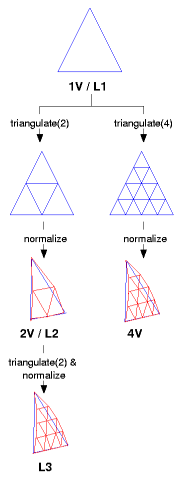Note: The common nV or nν notion introduced by Fuller looks alike, but those are derived from the original triangles, whereas L2 is derived from the already geodesized L1. I will later discuss the advantages and disadvantages of nV vs Ln in more details. The Ln vertices are normalized (spherisized or spherical projected) to 1, so r = 1 or d = 2. Triangulation Methods/Classes Triangulation Methods There are multiple ways to triangulate a triangle, the class 1 / alternate is the most prominant (creating 4 triangles), the class 2 / triacon (creating 6 triangles) is also well known, and I added the centerpoint (creating 3 triangles) and the slashing (creating 2 triangles, 3 possible ways) for sake of completeness. 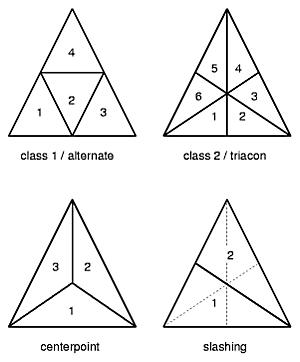Yet, for now I only focus on the class 1 / alternate and class 2 / triacon methods or classes. A more detailed overview of classes and methods is covered in Geodesic Math by Jay Salsburg. Class 1 / Alternate Subdivision Icosahedron 1V/L1 Icosahedron L2 (pre-normalized) Icosahedron L2 or 2V The class 1 or alternate subdivision provides a very even distribution of the triangles, alike the original triangle. Class 2 / Triacon Subdivision Icosahedron 1V/L1 Icosahedron L2T (pre-normalized) Icosahedron L2T or 2V Triacon The class 2 or triacon subdivision provides more options to cut the resulting sphere into a dome, yet, adds also one strut per triangle to an existing junction. E.g. a 5-way connector (with 5 triangles) triaconized results in 10-way connector, which in real-life poses a challange to implement, e.g. with a complex and rather large hub. For triacon subdivision I add 'T' to the existing notion, e.g. L1T is a L1 with triacon subdivision. As you notice, depending which kind of subdivision is used, the possible cut for a dome variant is completely different. Where suitable, I also rendered the dome / hemisphere option. The overview here has become very comprehensive already within a short time since I started worked on it, and I plan to extend it further. Please Note: I may change the notion from L1/2 to another more general approach later again; I likely stick with it as there is a clear distinction between nV and Ln notion You can calculate for each dome variant the strut lengths, edit the yellow field and hit ENTER to calculate the struts For more detailed variants, e.g. 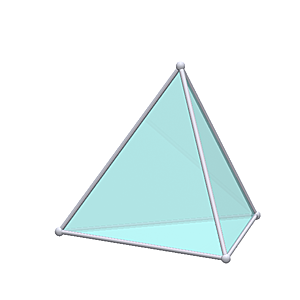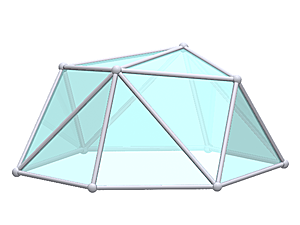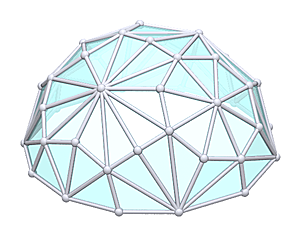fine triangulation and more options see my Geodesic Dome Notes Geodesic Tetrahedron Tetrahedron Tetrahedron Uniform Polyhedron: U1 Platonic Solid Platonic Element: Fire Wythoff symbol: 3|2 3 Symmetry Group: {3, 3, 3} Vertex Configuration: tetrahedral Dual: tetrahedron V: s3 / 12 * √2 A: s2 * √3 rinner: s / 12 * √6 router: s / 4 * √6 h: s / 3 * √6 Vertices/Connectors: 4 (3-way) Faces: 4 (3-sided) Edges/Struts: A x 6: 1.63299 I tried to "geodesize" using class 1 / alternate method the Tetrahedron into a sphere but you get a distorted sphere, no dome possible. And when the Tetrahedron solely is used as direct dome too many struts occur, L1 4 strut lengths and L2 already 12 strut lengths - not suitable. So, I won't even list all the details. 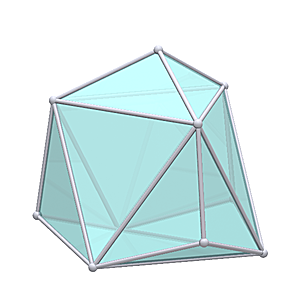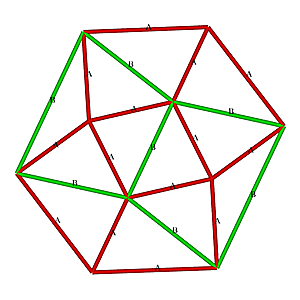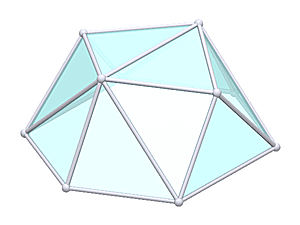Geodesic Tetrahedron L2 Geodesic Tetrahedron L3 Surprisingly when I "triaconized" the Tetrahedron, it turned out to be quite more suitable: Geodesic Tetrahedron L2T Geodesic Tetrahedron L2T Vertices/Connectors: 14 6 x 4-way 8 x 6-way Faces: 24 (3-sided) Edges/Struts: A x 24: 0.91940 B x 12: 1.15470 total 36 struts (2 kinds) strut variance 25.7% Geodesic Tetrahedron Dome L2T Geodesic Tetrahedron Dome L2T Geodesic Tetrahedron Dome L2T Vertices/Connectors: 10 2 x 3-way 6 x 4-way 2 x 6-way Faces: 12 (3-sided) Tetrahedron Dome L2T Construction Map Edges/Struts: A x 14: 0.91940 B x 7: 1.15470 total 21 struts (2 kinds) strut variance 25.7% d= A= x 14, B= x 7, 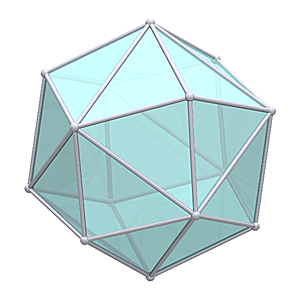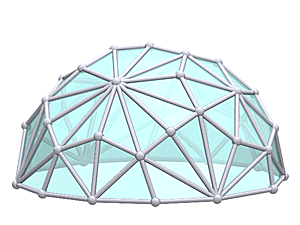It looks like a prepared (reduced to triangles using centerpoint triangulation) cube at the first sight. Geodesic Tetrahedron L3T Geodesic Tetrahedron L3T Vertices/Connectors: 74 36 x 4-way 24 x 6-way 6 x 8-way 8 x 12-way Faces: 144 (3-sided) Edges/Struts: A x 24: 0.29239 B x 48: 0.35693 C x 48: 0.47313 D x 24: 0.48701 E x 24: 0.60581 F x 48: 0.66092 total 216 struts (6 kinds) strut variance 126.4% Geodesic Tetrahedron Dome L3T Geodesic Tetrahedron Dome L3T Geodesic Tetrahedron Dome L3T Vertices/Connectors: 43 6 x 3-way 15 x 4-way 2 x 5-way 12 x 6-way 4 x 7-way 2 x 8-way 2 x 12-way Faces: 72 (3-sided) Tetrahedron Dome L3T Construction Map Edges/Struts: A x 12: 0.29239 B x 24: 0.35693 C x 28: 0.47313 D x 12: 0.48701 E x 14: 0.60581 F x 24: 0.66092 total 114 struts (6 kinds) strut variance 126.4% d= A= x 12, B= x 24, C= x 28, D= x 12, E= x 14, F= x 24, Next Page >> Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Content: Page 1: Introduction, Geodesic Procedure, Triangulation Methods/Classes, Class 1 / Alternate Subdivision ... Page 2: Geodesic Truncated Tetrahedron Page 3: Geodesic Octahedron Page 4: Geodesic Cube Page 5: Geodesic Cuboctahedron Page 6: Geodesic Truncated Octahedron Page 7: Geodesic Truncated Cube Page 8: Geodesic Rhombicuboctahedron Page 9: Geodesic Truncated Cuboctahedron Page 10: Geodesic Snub Cube Page 11: Geodesic Icosahedron Page 12: Geodesic Dodecahedron Page 13: Geodesic Icosidodecahedron Page 14: Geodesic Truncated Icosahedron Page 15: Geodesic Truncated Dodecahedron Page 16: Geodesic Rhombicosidodecahedron Page 17: Geodesic Truncated Icosidodecahedron Page 18: Geodesic Snub Dodecahedron Page 19: Geodesic Pentakis Dodecahedron, Pentakis Dodecahedron vs Geodesic Dodecahedron L1, Epcot Spaceship Earth ... Home   ·   About   ·   Tipi   ·   Yurt   ·   Dome   ·   Features   ·   Gallery Print   ·   Bookmark Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source