|
Star Dome Diarywritten by Rene K. Mueller, Copyright (c) 2006, last updated Thu, May 17, 2007
For now I'm still in the early planning stage. The Dome: Numbers & Material
The dome in numbers & materials:
Leaf-Like CoversAs I pointed out the leaf-like approach for the covers (rain, interior and also thermal insulation) is my preferd choice, with 5 leafs, and as I wrote in Star Dome you can make two halfs for the leaf to orient so that it results in a more narrow lane/stripe. Rain Cover: leaf geometry 5m long and 4m wide; by composing two halfs, you are able to have length 5m, and wideness 2.83m without extra space for the seam. So, I add some per seam 2cm, this makes 4x 2cm = 8cm, 2.91m total. My source of PE rain cover provides 3.1m wide and 20m long blanket, which gives 4 leafs, the 5th leaf will be 4m x 5m. If I make all 4 or 5 leafs using two halfs, I end up having 10 seams, likely the two fold seam. The last leaf, which is 4m wide gives me 1m extra, which I think is sufficient to have extra space when I make the winter thermal insulation 15cm thick, which means the diameter is 30cm larger, circumference increases by 1m then (0.30m * π). Since the pipes are 3.2cm, and junctions have 4 pipes overlayed each other, makes 4 x 3.2cm = 12.8cm per just knot or junction, which increases circumference by 2 * 12.8cm * π = 80cm each - since we have a couple of such junctions it would make sense to use as 5th leaf 5m x 5m, or have wider leafs in general. Interior Cover: I have a source of raw cotton, 1.5m wide, 10m long a roll. Per leaf 3 lanes/stripes: 4m + 3.6m + 2.4m ( + 0.6m), the last lane might not be required as there will be the skylight - 10m total per leaf (I may have to add 1-2cm per seam, which makes additional 10cm I should add; since I don't know how the crossing bows behave the total circumference, I like to add extra 5%: 4.2m + 3.78m + 2.52m = 10.50m, for all 5 leafs = 52.50m, it would require 6 rolls; but I'm thinking maybe I can patch a leaf with 10m alone, and reuse the cut-offs, have to think of a good way to do this (illustration follows). Thermal Insulation: using jute as blanket, and straw or hemp to fill with, source of 1.60m wide lanes of jute I have, but calculating with 1.5m as 10cm will be used for the seam, so 4m + 3.6m + 2.4m (+ 0.6m) (and add 5% to each) - so each lane would be a compartment, to fill the insulator with, plus quilting it each 20-40cm as well. I either tighten the rain cover to have the thermal insulation not move, or I use ropes outside like in case of the yurt. Detailed illustrations and photos will follow once I started to build it. Bamboo-based SkeletonThe original way to do the Star Dome is to use 10cm diameter bamboo, and split it into 6 splits. The wholesale garden company where I've got my bamboo for the yurt also sells bamboo with 10cm diameter, as decorative bamboo. It's rather expensive (e.g. CHF 70 / &euro 45 a piece). Pricing / LeftoversI quickly calculated several options (see in the following diary of 2006/8/26 for more details):
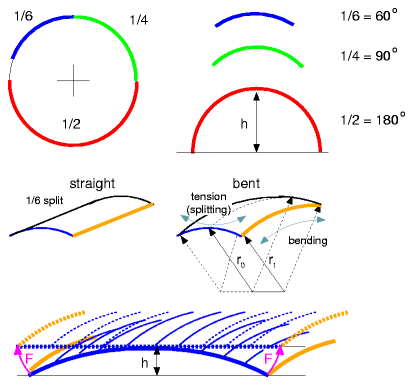
The best is to have 40cm to 100cm leftover used to overlap the splits and bind them together. The 3.6m long and 28/30mm diameter bamboo seems best in regards price and leftover: 1m left over, 3 pieces bind together, two junctions (1m/2 = 50cm overlapping). With 50 poles I can build two dome skeletons. The 6m long is the best in regards of stability, the 6 splits give 5.2cm wide or 60° of 10cm split piece, the likelyness of splitting it again due tension is smallest. To have just 180° increases the chance of additional splits when bent. Tests I made showed that 180° splits split 2 to 3 times when under tension and weaken the overall static. Tension with Bending within the SplitLet's go into some details of the bamboo split:
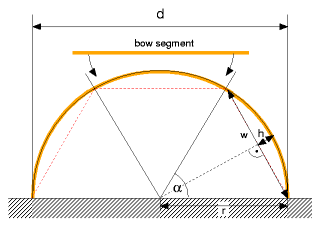
r = d / 2 w = ( (sin(α) r)2 + ((1-cos(α)) r)2)1/2 h = r - (r2 - ( w/2 )2)1/2
Homemade 1/2 SplitterBelow some tests I made with bamboo, here first a small homemade splitter. I made a 28mm hole, and put a swiss army knife so the blade faced the inside the hole, and fixated it.  Self-made bamboo splitter, one blade 2006/08/26 15:41  2006/08/26 15:41  2006/08/26 15:41 and then I pushed a 3m bamboo 24mm diameter through it:  Pulling/pushing a bamboo through . . . 2006/08/26 15:30  2006/08/26 15:34  2006/08/26 15:39  2006/08/26 15:40  Final two splits . . . 2006/08/26 15:41 First I made a test with a thinner bamboo and realized the hole must be just about diameter of the bamboo (plus apprx.4mm), if the bamboo is much smaller than the risk is that it won't split it half as in my test setup, but 1/3 to 2/3 which is not wanted. So I'm thinking to make dedicated bamboo splitters then when I sorted the bamboo. To keep in mind, the bamboo is usually sold sorted, the thicker ends (e.g. 20 to 22mm or 20/22mm), and smaller ends can be quite narrow (not defined really). Conclusion: I realized with a quick test that 1/2 split the bamboo is too weak and "break", it doesn't really break but creates more splits, e.g. 2 or 3 when under tension and the static is then not suitable anymore, that's why at least 1/4 or 1/6 splits should be used. Pipe-based Skeleton
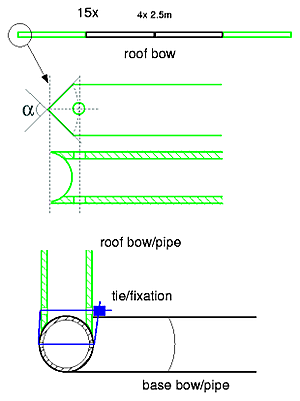
So I choose PE (Polyethylen) pipes, 5m long, 32mm outer diameter, 3mm thick, black. I will cut the 5m into 2x 2.5m long pipes, and combine 4x 2.5m to have a 10m bow then. 17x 10m bow, 17 * 4 = 68 x 2.5m pipes. In order to cover the black pipe, I thought using cotton to cover all of the pipe: c is 3.2cm * π +10% = 11cm + 0.5cm = ~12cm. Since I have access 1.5m wide and 10m long raw cotton, I can cover 12 bows with such a one roll.
I'm considering to put a cord through all bows (4 parts), and when the pipe junction is removed so all 4 parts of a bow remain associated.
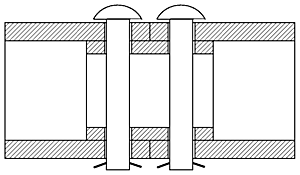
α can vary, e.g. 90° or more narrow if we have multiple bows (like in case of the Star Dome we have three bows per connection) - which the test below should show.
 Pipe junction: hole + 80-90° angle (evenly two sided) 2006/06/30 13:21  Pipe junction (side view) 2006/06/30 13:21  One pipe junction (60°) 2006/06/30 13:24  Three pipe junctions: 90° & 2x 45° 2006/06/30 13:27  Fixating pipes (1) 2006/06/30 13:28  Fixating pipes (2) 2006/06/30 13:31  Fixating pipes (3) 2006/06/30 13:32
The middle 90° pipe I cut 45° twice, and the other two pipes I made more narrow. I used simple plastic binder for this test, for a real life application I may still consider it just larger version of it, or metal binder, or use an smart way to bind with a cord.
It also needs to be noted that the test fixation does not provide any stability in regards of angle, vertical or horizontal, it does provide stability for pulling and pushing.
Tension of Bow SegmentsLet's look at the full bow, applies to bamboo or pipe too, composed by n-segments, e.g. 3 segments:
The formula for the h is the same as above for the bamboo splits, this time it's over full length of the bow: r = d / 2 w = ( (sin(α) r)2 + ((1-cos(α)) r)2)1/2 h = r - (r2 - ( w/2 )2)1/2
Let's provide a calculator for that (edit the numbers with yellow background and hit RETURN to calculate):
Bow Tension CalculatorMore detailed tension I will calculate later, for now h should give already an idea, and w vs lsegment is the length compression applied. I use this calculator to test bow segments of different fabrics: bamboo splits (1/2 and 1/4) and synthetic pipes. References:
ProcedureSince I realized I don't know yet for sure how the circumference is influenced by having 3.2cm diameter pipes, whether by interwaving the pipes diameter remains 6.4m or not, I will acquire the pipes or bamboo first, erect the skeleton of the dome, and measure the overall diameter and radii at each 50cm height (like to do when calculating a free form dome). I'm still pondering on bamboo and synthetic pipes and make some tests with one bow (10m) with 2-3 segments (5-3m each) with various material - and probably make a bamboo based skeleton and a PVC pipe based skeleton and test it for a couple of months. Content:
|
| Home | · | About | · |  Tipi | · |  Yurt | · |  Dome | · | Features | · | Gallery |
Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller
Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm
Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source