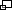Home   ·   About   ·   Tipi   ·   Yurt / Ger   ·   Dome   ·   Features   ·   Gallery About Overview License Tipi Overview Tipi Diary Yurt / Ger Overview Yurt Notes & Calculator Yurt / Ger Diary Yurt Builder Conference Living Notes Material Notes Dome Overview Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Features Overview Chris Aeppli Claudius Kern René K. Müller Geodesic Solitude Johnny's Capsule Geodesic Clay Mud Dome Jurtendorf (Switzerland) Neolithics of Pfyn Strawbale Cabin Dome Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Bow Dome Types Bending the Bows Crown & Crownless Canvas Symbols & Formulas Bow Dome Calculator Bow Dome Model Crownless Bow Dome Willow Bow Dome Dome in Fessenheim Miscellaneaus Bow Domes Links Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Site Search Enter term & press ENTER If you found the information useful, consider to make a donation:   Page << Prev | 1 | 2 | Next >> Bow Dome written by Rene K. Mueller, Copyright (c) 2006, 2007, last updated Sat, May 24, 2014 Updates Thu, July 19, 2007: Cleaned up the article, and added "bow dome typology" to provide more systematic of variants, also enhanced the bow dome calculator. . Tue, April 18, 2006: Added more full length bows (reaching entire half sphere) models in Misc Domes. . Sun, February 19, 2006: Lot's of improvements, bow calculator using bezier curves, canvas caculator, and notes. . Sun, January 8, 2006: First version with a couple of bow dome types. . Bow Dome Model, composed by bamboo splits, apprx. 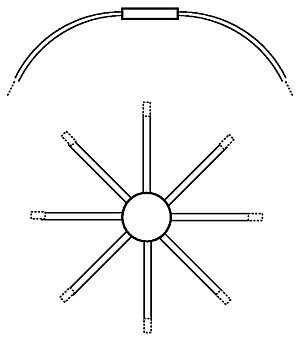3/8 sphere The bow dome goes back to the very first habitat built by humans to shelter himself - composed by flexible and rather thin tree branches, can be thereby considered an archaic form of habitat aside of the tipi. Bow Dome Types For a start a few different types of bow domes, derived from the bow bending, tying and assembling: The Wigwam and Star Dome are not covered in this section, but have dedicated pages, but according this typology also considered "Bow Domes". This typology is subject of change, as I still search for a common mathematically description for all bow-based domes, which takes in account also the bow tying options as illustrated above. See also the broader overview of Strut/Bow-based Building Typology, and also miscellaneous bow domes models I made. 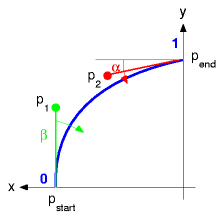The Model Bow Dome Bezier Curve Model I'm using a simple mathematical model based on Bezier curve with two angles, α and β which define the bending of both ends - it helps to describe the bow domes more precise, and later on this page also a "bow dome calculator" provides the numerical solution for those types, including canvas shapes for a leaf-like composed cover. p(x,y) = fbezier(t) t = 0 .. 1 pstart = (1,0) (bottom) pend = (0,1) (top) p1 = (1-sin(β)*.6,cos(β)*.6) p2 = (cos(α)*.6,1-sin(α)*.6) fbezier(t) = (1-t)3 pstart + 3 t (1-t)2 p1 + 3 t2 (1-t) p2 + t3 pend Let's have a look to the different dome approaches with this model. 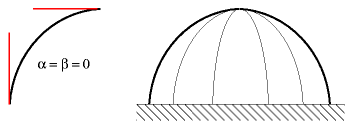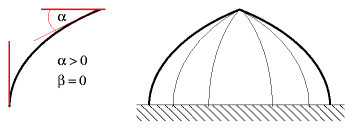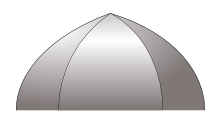Half Sphere / Hemisphere / Unibow / Layover-Tie Dome Both α & β are zero, so the resulting dome is a half sphere. Half Sphere Bow Dome This form is the most common and expected, yet, it has some disadvantages, e.g. that the roof angle at the top is almost horizontal. In case of rain or even snow it may not naturally slide or flow away. So it often is suitable to add another smaller acrylic dome as skylight to avoid these challenges. Cross-Tie Bow Dome α is greater than 0°, β can be 0° or positive, or negative, either way it will form a pointy dome. Cross-Tie Bow Dome This form is in particular suitable for regions with lot of rainfall, to have on top a certain angle already to make sure rain does not last too long in order to penetrate the cover (e.g. canvas or plaitwork). An example are the Sidama (Ethiopia highland region) Tukul houses. They are composed by a bamboo split plaitwork, built by specialized handicraft groups. 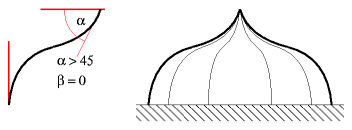Peak-Tie Bow Dome α is greater than 45°, β remains 0. 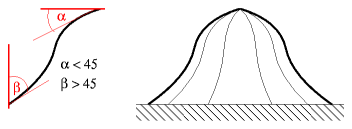Peak-Tie Bow Dome Bell Bow Dome α is less than 45°, β greater than 45° Bell Bow Dome Other Types Anyway, there are more options, as the bow can be bent not just one way (outward or inward), but a combination of both and so more variants are possible, but then also the resulting required cover form becomes quite challenging to plan. Bending the Bows Prefabricated Bows Wood can be bent within boiled water like a steam chamber easily, more details later. Other materials such as aluminium or sheet metal might allow natural bending without breaking. 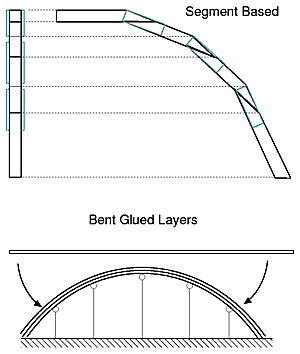Modern bow domes have prefabricated struts composed by several segments making up a bent bow, e.g. like the example as shown on the right, 4 segment bow with enforcement strut on left and right side of the composition; or multiple layers of thin wooden layers (0.2-0.5 cm) bent and glued together. Crown & Crownless The bows need to be bind together at the top, and one good approach is a small wheel where all bows enter, tied, or fixated with a screw. As comparison take also a look at the wigwam, where the bows have different diameters, and are bound at the intersections, and no crown required. I had the idea to make a "crownless" yurt, and the same may be appliable to the bow dome as well I tought: laying the poles over each other in order to have no crown holding the roof poles. I made this test with 40cm long bamboo split (4mm diameter), and the test was successful as you see. On the next page, where I documented making models, you will find more photos of this "crownless" bow dome model. Canvas The tricky part is the canvas for the outer layer (e.g. rain canvas) for the bow domes. Along the bows the canvas forms leaf-like segments so it rather obvious to compose the canvas by such, more below. 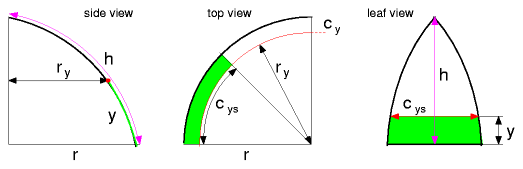Symbols & Formulas y = 0 .. h cy = ry * 2 * π h = fh(α,β,r) ynorm = y / h cys = cy / nleaves ry = fr(α,β,ynorm) fr(α,β,ynorm) is different for each dome type, for a half-sphere dome: fr(α,β,ynorm) = cos( ynorm * 90 ) * r fh(α,β,r) = r * 2 * π / 4 For a general approach I simplified it using Bezier curve to simulate the bending of a bow. Industrial manufactured bows are done via wooden segments, the following Bow Dome Calculator gives you the exact measurements also to construct the bend bow via segments. In case you use natural bending materials, you may still have to calculate your canvas by hand by measuring each radius at a given height (refere the illustrations above). Bow Dome Calculator Edit diameter d, height h, amount of leaves of the cover nleaves and the two angles α and β, and then hit "calculate". d = m, h = m, nleaves = , α = °, β = °, show overviewdetail, Hint: half sphere: α = β = 0, pointy: α = 40, β = 0, pointy inverted: α = 60, β = 90 Outline Bow Dome Sketch, Human is 170cm height Cover / Canvas Surface Currently not available, back soon. (Bug in the calculation when d/2 > h, fixed in a few days 2014/05/24) Leaf composition: interior & rain canvas Sewing the Cover In order to sew these leave-like sphere surface together as rain cover, the water leak is particular to be avoided and so special care of how to sew the seams together: Options of Seam Sewing In case of the bow dome a combination of two of the options might be used: overlay horizontal canvas stripes or lanes to compose a part of a roof leaf or segment use either one-fold or two-fold to patch the leaves / segments together Consider to seal the stitching holes from sewing with silicon or good clear tape for canvas (with threads) and preferable use water-resistant sewing thread as well. Next Page >> Page << Prev | 1 | 2 | Next >> Content: Page 1: Bow Dome Types, The Model, Half Sphere / Hemisphere / Unibow / Layover-Tie Dome, Cross-Tie Bow Dome ... Page 2: Bow Dome Model, The Skeleton, The Rain Cover, Crownless Bow Dome, Willow Bow Dome, Dome in Fessenheim ... Home   ·   About   ·   Tipi   ·   Yurt   ·   Dome   ·   Features   ·   Gallery Print   ·   Bookmark Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source