|
Site Search
If you found the information useful, consider to make a donation:
| |
written by Rene K. Mueller, Copyright (c) 2007, last updated Wed, January 9, 2008
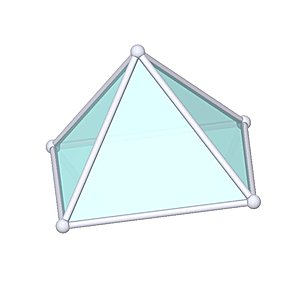
 Square Pyramid |
- Johnson Solid: J1
- Vertices: 5
- Faces: 5
- Edges: 8
- V: s3 / 6 * √2
- A: s2 * (1 + √3)
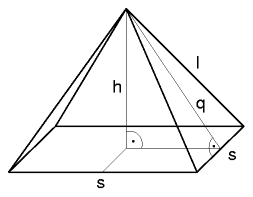
General Pyramid |
The general pyramid:
- q = √((s/2)2 + h2)
- l = √((s/2)2 + q2)
- A = 2 s q + s2
- Awall/roof = 2 s q
- V = s2 h / 3
Most obvious association with pyramids comes from the egyptian pyramids in Giza and those of the mayans in south america.
It is also apparent those pyramids have been built with enormous effort and skills which is now honored by the durability of thousands of years.
The largest pyramid in Giza is the Khufu Pyramid, with following values:
- s = 231m (original) (now: 230.4m)
- h = 146.6m (original) (now: 138.8m)
thereby
- q = 186.632m
- l = 219.478m
Interesting ratio:
- s/h = 1.57571.. ~ π/2 ~ 11/7
Read more at Great Pyramid of Giza  . .
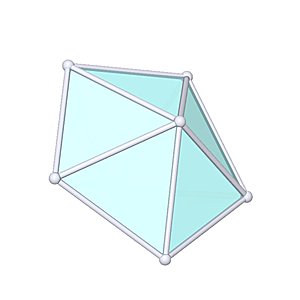
 Pentagonal Pyramid |
- Johnson Solid: J2
- Vertices: 6
- Faces: 6
- Edges: 10
- V: s3 / 24 * (5 + √5)
- A: s2 / 2 * √(5/2 * (10 + √10 + √(75+30*√5))
The roof isn't very steep, unless those roof struts would be made longer - it would be a very simplistic habitat.
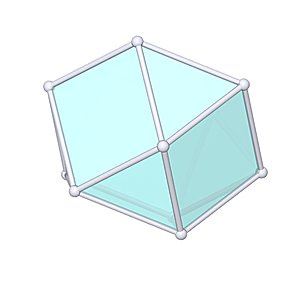
 Triangular Cupola |
- Johnson Solid: J3
- Vertices: 9
- Faces: 8
- Edges: 15
- V: s3 * (5/(5*√2))
- A: s2 * (3+5/2*√3)
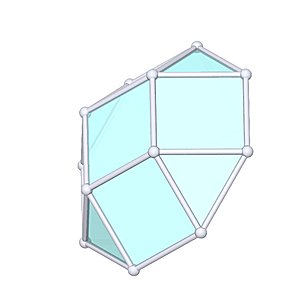
 Square Cupola |
- Johnson Solid: J4
- Vertices: 12
- Faces: 10
- Edges: 20
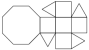
Also cap of a Rhombicuboctahedron.
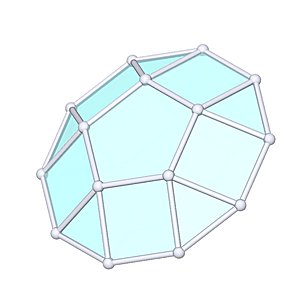
 Pentagonal Cupola |
- Johnson Solid: J5
- Vertices: 15
- Faces: 12
- Edges: 25
- V: s3 / 6 * (5+4*√5)
- A: s2 / 4 * (20+√(10*(80+31*√5+√(2175+950*√5))))
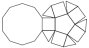
Also cap of a Rhombicosidodecahedron.
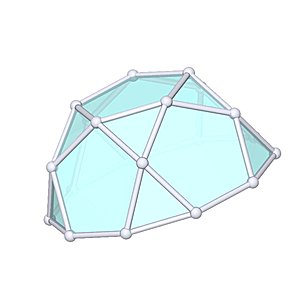
 Pentagonal Rotunda |
- Johnson Solid: J6
- Vertices: 20
- Faces: 17
- Edges: 35
- V: s3 / 12 * (45+17*√5)
- A: s2 * 5/2 * (√3+√(26+(58/√5)))
- h: s * √(1/5*(5+2*√5))
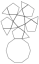
Also 1/2 of a Icosidodecahedron.
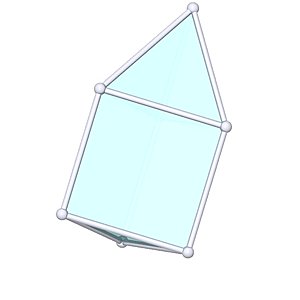
 Elongated Triangular Pyramid |
- Johnson Solid: J7
- Vertices: 7
- Faces: 7
- Edges: 12
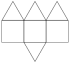
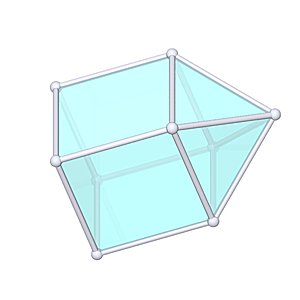
 Elongated Square Pyramid |
- Johnson Solid: J8
- Vertices: 9
- Faces: 9
- Edges: 16
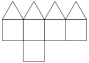
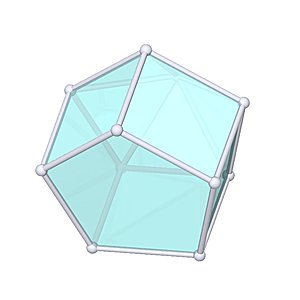
 Elongated Pentagonal Pyramid |
- Johnson Solid: J9
- Vertices: 11
- Faces: 11
- Edges: 20
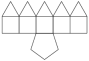
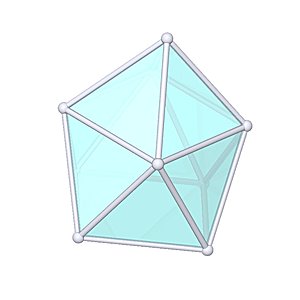
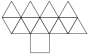
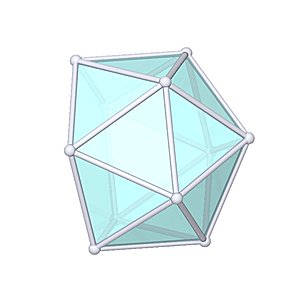
 Gyroelongated Square Pyramid |
- Johnson Solid: J10
- Vertices: 9
- Faces: 13
- Edges: 20
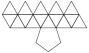
 Gyroelongated Pentagonal Pyramid |
- Johnson Solid: J11
- Vertices: 11
- Faces: 16
- Edges: 25
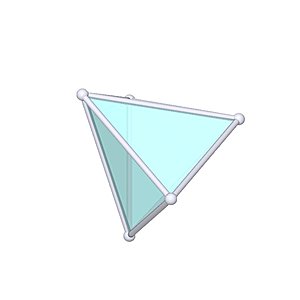
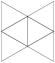
 Triangular Dipyramid |
- Johnson Solid: J12
- Vertices: 5
- Faces: 6
- Edges: 9
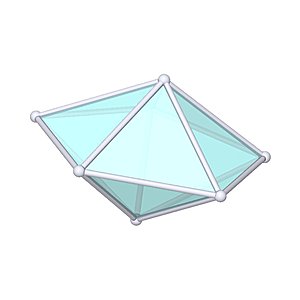
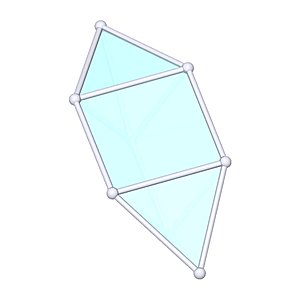
 Pentagonal Dipyramid |
- Johnson Solid: J13
- Vertices: 7
- Faces: 10
- Edges: 15
- V: s3 / 12 * (5 + √5)
- A: s2 * 5/12 * √3
- router: s / 10 * √(50+10*√5)
- h: s / 10 * √(50-10*√5)

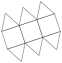
 Elongated Triangular Dipyramid |
- Johnson Solid: J14
- Vertices: 8
- Faces: 9
- Edges: 15
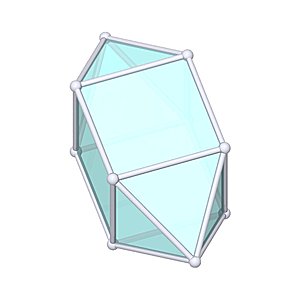
 Elongated Square Dipyramid |
- Johnson Solid: J15
- Vertices: 10
- Faces: 12
- Edges: 20
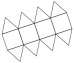

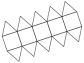
 Elongated Pentagonal Dipyramid |
- Johnson Solid: J16
- Vertices: 12
- Faces: 15
- Edges: 25

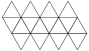
 Gyroelongated Square Dipyramid |
- Johnson Solid: J17
- Vertices: 10
- Faces: 16
- Edges: 24
- V: s3 * 2(1/4) / 4 * (1 + √2 + 2(1/4) )
- A: s2 * 4 * √3
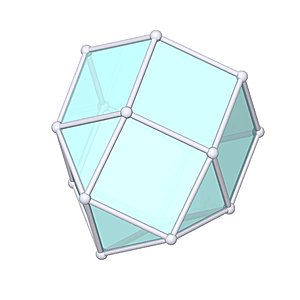
 Elongated Triangular Cupola |
- Johnson Solid: J18
- Vertices: 15
- Faces: 14
- Edges: 27
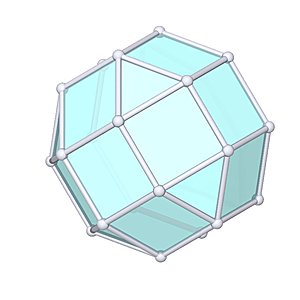
 Elongated Square Cupola |
- Johnson Solid: J19
- Vertices: 20
- Faces: 18
- Edges: 36

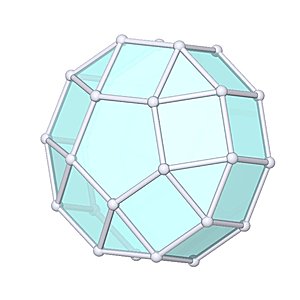
 Elongated Pentagonal Cupola |
- Johnson Solid: J20
- Vertices: 25
- Faces: 22
- Edges: 45
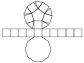
 Elongated Pentagonal Rotunda |
- Johnson Solid: J21
- Vertices: 30
- Faces: 27
- Edges: 55
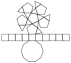
Very suitable for a habitat, the top smaller pentagon as skylight, and eventually the side pentagons further triangulated each.
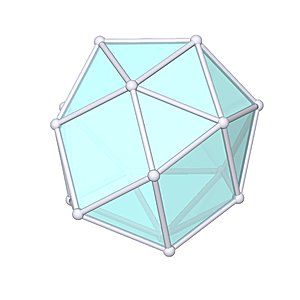
 Gyroelongated Triangular Cupola |
- Johnson Solid: J22
- Vertices: 15
- Faces: 20
- Edges: 33
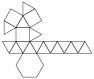
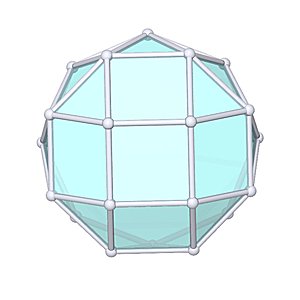
 Gyroelongated Square Cupola |
- Johnson Solid: J23
- Vertices: 20
- Faces: 26
- Edges: 44
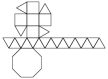
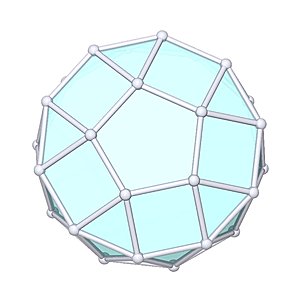
 Gyroelongated Pentagonal Cupola |
- Johnson Solid: J24
- Vertices: 25
- Faces: 32
- Edges: 55
Next Page >>
Content: - Page 1: Introduction, Platonic Solids, Archimedean Solids, Tetrahedron, Truncated Tetrahedron, Octahedron ...
- Page 2: Johnson Solids
- Page 3: Square Pyramid, Historic Pyramids, Pentagonal Pyramid, Triangular Cupola, Square Cupola, Pentagonal Cupola ...
- Page 4: Gyroelongated Pentagonal Rotunda, Gyrobifastigium, Triangular Orthobicupola, Square Orthobicupola ...
- Page 5: Augmented Triangular Prism, Biaugmented Triangular Prism, Triaugmented Triangular Prism ...
- Page 6: Parabigyrate Rhombicosidodecahedron, Metabigyrate Rhombicosidodecahedron, Trigyrate Rhombicosidodecahedron ...
- Page 7: Uniform Polyhedra, References
- Page 8: Waterman Polyhedra, Some More Examples, Different Origins, Features of Waterman Polyhedra ...
|



























































