If you found the information useful, consider to make a donation:
written by Rene K. Mueller, Copyright (c) 2007, last updated Fri, February 25, 2022
Snub Cube
Uniform Polyhedron: U12
aka Cubus Simus
aka Snub Cuboctahedron
Archimedean Solid: A7
Wythoff symbol: |2 3 4
Symmetry Group: octahedral
Vertex Configuration: {3, 3, 3, 3, 4}
Dual: pentagonal icositetrahedron
t: 1/3 * (1 + (10-3*√33)(1/3) + (19+3*√33)(1/3) )
V: s3 * ( 8/3 * √(3 * (3-t)/(4*(2-t)) - 1) + √(4 * (3-t)/(4*(2-t)) -2) )
V: s3 * √((613 * t + 203)/(9*(35*t-62)))
A: s2 * (6 + 8 * √3)
rinner : s * √(abs(1-t)/(4*(2-t)))
router : s * √((3-t)/(4*(2-t)))
Vertices/Connectors: 24 (5-way)
Faces: 38
Edges/Struts:
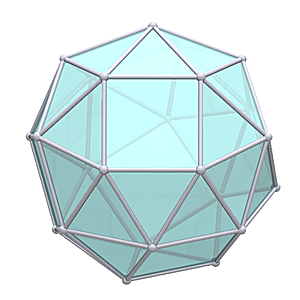
Geodesic Snub Cube L1
Vertices/Connectors: 30
Faces: 56 (3-sided)
Edges/Struts:
A x 24: 0.54710
B x 60: 0.74421
total 84 struts (2 kinds)
strut variance 36.0%
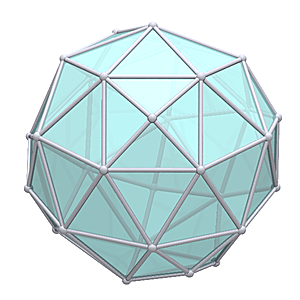
Geodesic Snub Cube L2
Vertices/Connectors: 114
Faces: 224 (3-sided)
Edges/Struts:
A x 48: 0.27620
B x 48: 0.28731
C x 120: 0.37897
D x 24: 0.38686
E x 96: 0.40089
total 336 struts (5 kinds)
strut variance 45.3%
Geodesic Snub Cube L2T
Vertices/Connectors: 170
84 x 4-way
56 x 6-way
6 x 8-way
24 x 12-way
Faces: 336 (3-sided)
Edges/Struts:
A x 24: 0.14348
B x 48: 0.20649
C x 96: 0.23304
D x 24: 0.26808
E x 48: 0.27620
F x 120: 0.37897
G x 48: 0.40339
H x 96: 0.44048
total 504 struts (8 kinds)
strut variance 207.7%
At the first sight it looks as if there is a horizontal base, yet, it's slightly distorted and unsuitable therefore for a dome consideration, unfortunately.
Next Page >>
Content :