|
Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Geodesic Polyhedrawritten by Rene K. Mueller, Copyright (c) 2007, last updated Fri, February 25, 2022
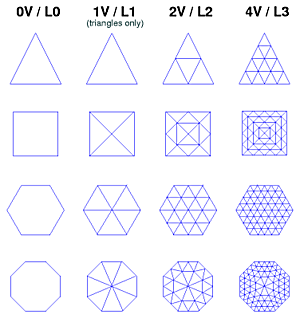
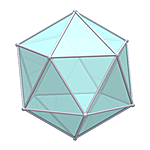
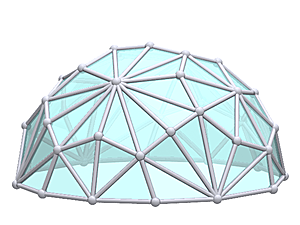
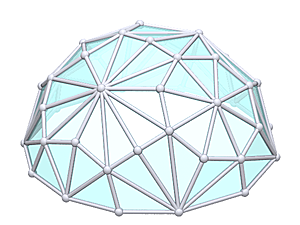
IntroductionAfter studying the geodesic dome (often direct associated to Buckminster Fuller but he wasn't the first), which essentially is derived from a Icosahedron, I thought to check the possibility to triangulate other platonic and archimedean solids. Based on the information I gathered from regular & semi-regular polyhedra I made this overview.Geodesic Procedure
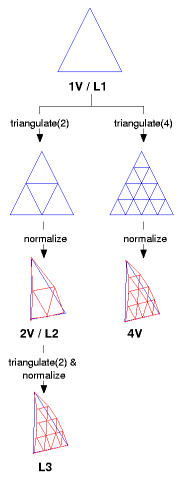
Note: The common nV or nν notion introduced by Fuller looks alike, but those are derived from the original triangles, whereas L2 is derived from the already geodesized L1.
I will later discuss the advantages and disadvantages of nV vs Ln in more details.
The Ln vertices are normalized (spherisized or spherical projected) to 1, so r = 1 or d = 2. Triangulation Methods/Classes
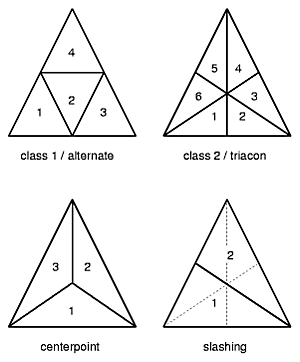
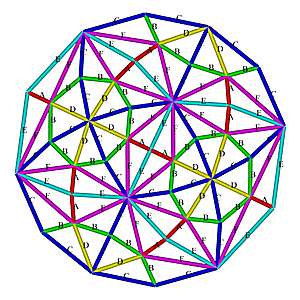
for sake of completeness.
Yet, for now I only focus on the class 1 / alternate and class 2 / triacon methods or classes.
A more detailed overview of classes and methods is covered in Geodesic Math Class 1 / Alternate Subdivision
The class 1 or alternate subdivision provides a very even distribution of the triangles, alike the original triangle.
Class 2 / Triacon Subdivision
The class 2 or triacon subdivision provides more options to cut the resulting sphere into a dome, yet, adds also one strut per triangle to an existing junction. E.g. a 5-way connector (with 5 triangles) triaconized results in 10-way connector, which in real-life poses a challange to implement, e.g. with a complex and rather large hub. For triacon subdivision I add 'T' to the existing notion, e.g. L1T is a L1 with triacon subdivision. As you notice, depending which kind of subdivision is used, the possible cut for a dome variant is completely different. Where suitable, I also rendered the dome / hemisphere option. The overview here has become very comprehensive already within a short time since I started worked on it, and I plan to extend it further. Please Note:
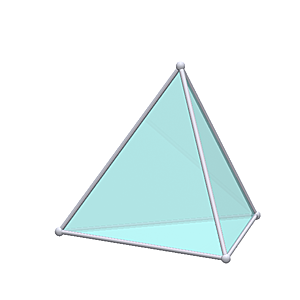
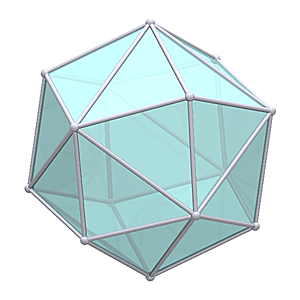
Geodesic TetrahedronTetrahedron
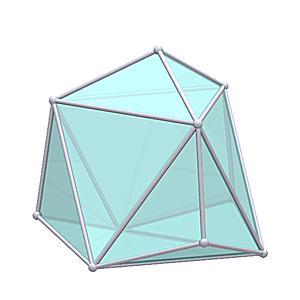
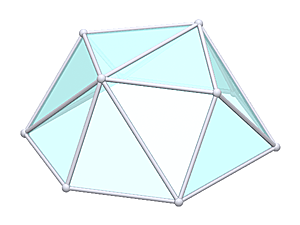
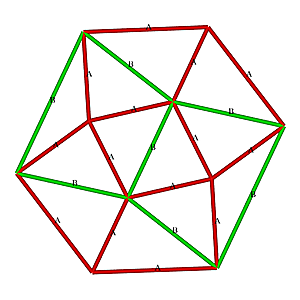
Surprisingly when I "triaconized" the Tetrahedron, it turned out to be quite more suitable: Geodesic Tetrahedron L2T
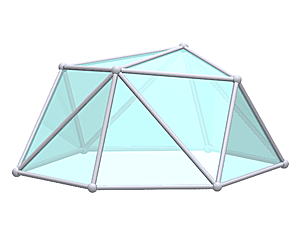
Geodesic Tetrahedron Dome L2T
It looks like a prepared (reduced to triangles using centerpoint triangulation) cube at the first sight. Geodesic Tetrahedron L3T
Geodesic Tetrahedron Dome L3T
Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | Next >> Content:
|
| Home | · | About | · |  Tipi | · |  Yurt | · |  Dome | · | Features | · | Gallery |

Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller
Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm
Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source