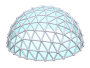
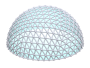
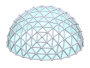
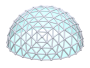
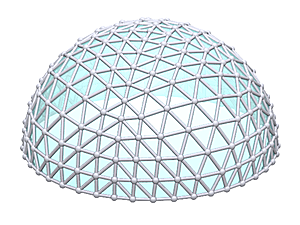
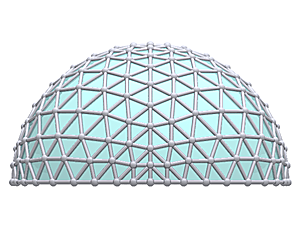
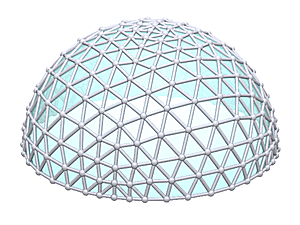
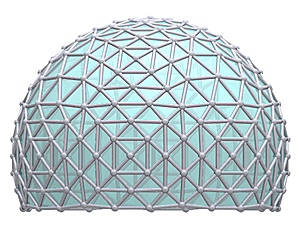
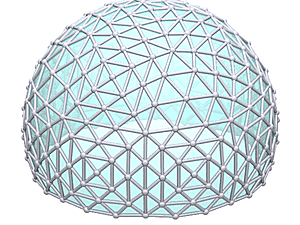
Welcome to my detailed and comprehensive geodesic domes notes, actually the 2nd version (total rewrite of the 1st version). Since it has become so long I include a table of content ahead.
Table of Content
- Table of Content
- Introduction
- Origin of the Geodesic Dome
- Geodesize: Triangulate & Normalize
- Procedure & Evolution of a Subdividing Triangle
- The nV Notion
- The Ln Notion
- The Concated V Notion
- The Concated V vs Ln Notion
- Normalizing
- References
- Overview of Variants
- How to Use the Notes
- Strut Options & Notion
- Wooden Strut with Flat Connector
- Wooden Strut with Pipe Hub
- Pipe/Tube based Strut
- Bamboo Strut
- Bending the Strut-Endings
- Detailed Calculation of the Faces or Hub/Strut Angles
- The Icosahedron
- 1V/L1 2/3 Icosahedron Dome
- 2V/L2 Icosahedron Dome
- 3V 4/9 Icosahedron Dome
- 3V 5/9 Icosahedron Dome
- 4V Icosahedron Dome
- L3 Icosahedron Dome
- 5V 7/15 Icosahedron Dome
- 5V 8/15 Icosahedron Dome
- 6V Icosahedron Dome
- 2V.3V Icosahedron Dome
- 3V.2V Icosahedron Dome
- 7V 10/21 Icosahedron Dome
- 7V 11/21 Icosahedron Dome
- 8V Icosahedron Dome
- L4 Icosahedron Dome
- The Octahedron
- 1V/L1 Octahedron Dome
- 2V/L2 Octahedron Dome
- 3V Octahedron Dome
- 4V Octahedron Dome
- L3 Octahedron Dome
- L3 1/4 Octahedron Dome
- L3 5/8 Octahedron Dome
- 5V Octahedron Dome
- 6V Octahedron Dome
- 2V.3V Octahedron Dome
- 3V.2V Octahedron Dome
- 7V Octahedron Dome
- 8V Octahedron Dome
- L4 Octahedron Dome
- L4 7/16 Octahedron Dome
- L4 9/16 Octahedron Dome
- 9V Octahedron Dome
- 3V.3V Octahedron Dome
- 10V Octahedron Dome
- 2V.5V Octahedron Dome
- 2V.5V Octahedron Dome
- The Cube
- Preparing the Cube
- 1V/L1 Cube Dome
- 2V/L2 Cube Dome
- 3V Cube Dome
- 4V Cube Dome
- L3 Cube Dome
- 5V Cube Dome
- 6V Cube Dome
- 2V.3V Cube Dome
- 3V.2V Cube Dome
- 7V Cube Dome
- The Cuboctahedron
- Preparing the Cuboctahedron
- 1V/L1 Cuboctahedron Dome
- 2V/L2 Cuboctahedron Dome
- 3V Cuboctahedron Dome
- 4V Cuboctahedron Dome
- L3 Cuboctahedron Dome
- 5V Cuboctahedron Dome
- 6V Cuboctahedron Dome
- 2V.3V Cuboctahedron Dome
- 3V.2V Cuboctahedron Dome
- The Truncated Octahedron
- Preparing the Truncated Octahedron
- 1V/L1 Truncated Octahedron Dome
- 2V/L2 Truncated Octahedron Dome
- 3V Truncated Octahedron Dome
- 4V Truncated Octahedron Dome
- L3 Truncated Octahedron Dome
- The Rhombicuboctahedron
- Preparing the Rhombicuboctahedron
- 1V/L1 3/8 Rhombicuboctahedron Dome
- 1V/L1 5/8 Rhombicuboctahedron Dome
- 2V/L2 3/8 Rhombicuboctahedron Dome
- 2V/L2 5/8 Rhombicuboctahedron Dome
- 3V 3/8 Rhombicuboctahedron Dome
- 3V 5/8 Rhombicuboctahedron Dome
- Building Models
- Real Life Application
- Options
- Connectors
- Separate Functions
- Cover
- 4/8 Sphere Cover Calculator
- Sewing the Cover
- 4V 4/8 Geodesic Dome Model with Cover
- Windows & Door
- Interior & Floor
- 2nd Floor
- Links
Changes
Following changes were made to previous versions:- 2nd version: Icosahedron, Octahedron, Cube, Cuboctahedron and Truncated Octahedron for each 1V to 6V or more triangulations, a few strut cutting optimization included. Be aware the notion of the strut types of Icosahedron 2V, 3V and 4V changed from previous version of the notes.
- 1st version: Icosahedron based domes covered in details: 2V, 3V and 4V with optimizations of cutting struts
Introduction
If you don't care about the origin, the notion, the mathematics behind the geodesic domes, skip right to the 3rd page.
Origin of the Geodesic Dome
  Construction of a planetarium of Carl Zeiss in Jena (Germany) 1922, planned by Walther Bauersfeld |
 's often used notion, but as pointed out before, Walther Bauersfeld
's often used notion, but as pointed out before, Walther Bauersfeld  created a "geodesic" dome in 1922 for Carl Zeiss in Jena (Germany), he even patented it in Germany 1925 (Patent Nr. 415395) as
seen in this page
created a "geodesic" dome in 1922 for Carl Zeiss in Jena (Germany), he even patented it in Germany 1925 (Patent Nr. 415395) as
seen in this page  , so well over 20 years before B. Fuller was developing the "geodesic" approach.
, so well over 20 years before B. Fuller was developing the "geodesic" approach.
The term "geodesic" is a mathematical term, which was adapted by Fuller to describe his approach, the term otherwise literally means "shortest path of two points on a sphere or curved space".
It seems Fuller simply wasn't aware of Bauersfeld prior work at Carl Zeiss, and reinvented and popularized it then in his life (1895 - 1983) and beyond via the Buckminster Fuller Institute  these days.
these days.
  US Pavilion at the Expo 1967 in Montreal (Canada) by Buckminster Fuller & Shoji Sadao |
 web-site by Tara Landry and her dome calculator.
The first version of my notes used the strut or chord factors she extracted from books by Hugh Kenner (Geodesic Math & How To Use It) and Lloyd Khan (Domebook I & II), who themselves relied on Fuller's work.
web-site by Tara Landry and her dome calculator.
The first version of my notes used the strut or chord factors she extracted from books by Hugh Kenner (Geodesic Math & How To Use It) and Lloyd Khan (Domebook I & II), who themselves relied on Fuller's work.
As a result of my study on geodesic polyhedra I wrote my own software tools to calculate, adjust and render 3D solids, such as platonic, archimedean and johnson solids, also generally known as regular and semi-regular polyhedra.
Based on that study of the manifold solids and their geodesic derivates I rewrote my "Geodesic Domes Notes" entirely with more variants (not just Icosahedron based domes) including dedicated calculators for each variant, optimization of cutting respective struts and a 2D construction map.
And as the time goes by I will add more comments on each featured dome variant.
Geodesize: Triangulate & Normalize
|
|
|
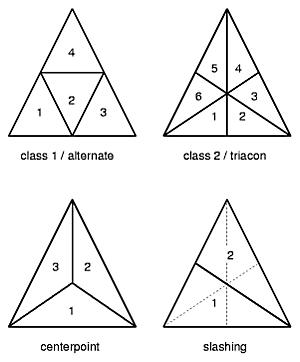  Triangulate Methods |
To triangulate a triangle there are different methods or classes available, most prominent are the class 1 or alternate, and class 2 or triacon; additionally several "methods" are distincted - read for more at the References, in particular Joseph D. Clinton's work for NASA.
Of course you can also subdivide into other than triangles, such as other polygonal forms. I focus as a first step on the triangulation and its "class 1" or "alternate" way.
Procedure & Evolution of a Subdividing Triangle
I have summarized several procedures incl. ones I discovered (some may have been used by others previously, I'm personally just not aware of it):
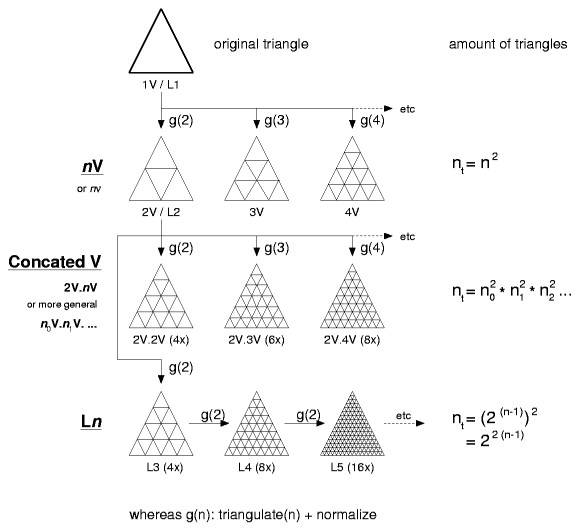 |
The nV Notion
Buckminster Fuller introduced the notion of nν often also written as nV (V like in "vision", whereas ν is the greek letter "nu"), it means the amount of division of an original triangle. In this case the class 1 or alternate method is used, and from the original triangle.Formulas:
nt = n2
Example:
5V or 5ν has 52 triangles per original triangle
The Ln Notion
More in an accident I "geodesized" an already geodesized solid, because the program I wrote could not make subdivisions other than 2 at first, so in order to create 4V I thought to pipe it into the same program twice - and as a surprise the strut lengths varied from the 4V notion - I also came up with 5 strut lengths and not 6 as common for the 4V.I realized then, the triangles were more even, smaller variance of strut lengths. In order to distinct this method from the nV notion I called it Level 1 or L1 and then L2. In order to make it more aligned with the nV notion: 1V and L1 are the same, 2V and L2 are also the same, but 4V and L3 differ then.
Formulas:
nt = (2(n-1))2 = 22(n-1)
Example:
L5 = (25-1)2 = 22(5-1) = 256 triangles per triangle
The Concated V Notion
While I discovered a geodesized geodesize solid (like L3) provides different strut lengths and variance than a comperable, in sense of amount of subdivisions nV variant, I extended that it wouldn't necessary be the 2V to derive others, so I introduce the n0V.n1V . . . notion, concate the procedure of geodesize with '.' together.
- 2V.2V ~ 4V
- 3V.2V ~ 6V
- 2V.2V.2V ~ 8V
Formulas:
nt = n02 * n12 * n22 ...
Example:
2V.3V.2V ~ 12V = 22 * 32 * 22 = 144 triangles per original triangle
The Concated V vs Ln Notion
|
Just for sake of completeness:
|
and also:
|
Normalizing
In order to normalize, we need to determine the distance of each vertice (x,y,z) from the center or an origin (xorigin,yorigin,zorigin):
d = √(x2 + y2 + z2)
or more general
d = √((x - xorigin)2 + (y - yorigin)2 + (z - zorigin)2)
To normalize we divide each of x, y and z by the distance:
x = x / d
y = y / d
z = z / d
or more general
x = (x - xorigin) / d + xorigin
y = (y - yorigin) / d + yorigin
z = (z - zorigin) / d + zorigin
which adjusts the point to have distance of 1 to the center - a sphere is a form where all points of the surface have the same distance to its center; so by normalizing the point is spherized or spherical projected.
There is far more math to cover in geodesic approaches, but for now I leave it at this and may extend it later more. A bit more math comes when calculating details of the required struts to compose a dome, this follows on the next page then.
References
- NASA Contractor Report: Advanced Structural Geometry Studies, Part I: Polyhedral Subdivision Concepts for Structural Applications
 by Joseph D. Clinton (1971)
by Joseph D. Clinton (1971)
- Geodesic Math
 by Joseph D. Clinton, rewrite by Jay Salsburg
by Joseph D. Clinton, rewrite by Jay Salsburg 
- Structural Design Concepts for Future Space Missions
 or "Geodesic Design Concepts" for NASA in 1968, by various authors incl. B. Fuller, rewrite by Jay Salsburg
or "Geodesic Design Concepts" for NASA in 1968, by various authors incl. B. Fuller, rewrite by Jay Salsburg
- Mother Earth News: Where Domes Come From
 (1971)
(1971)
The next pages go into the details of the geodesic domes variants.
Overview of Variants
Since the possibilities are so vast I have selected a couple of platonic and archimedean solids - as I previously studied in Geodesic Polyhedra - which seem reasonable for dome constructions, and created variants with up 1000 struts, and max 30 different strut lengths. So, these are the results:
Icosahedron-based Geodesic Domes
|
|
|
|
| ||||||||||
|
|
|
|
| ||||||||||
|
|
|
|
Octahedron-based Geodesic Domes
|
|
|
|
| ||||||||||
|
|
|
|
| ||||||||||
|
|
|
|
| ||||||||||
|
|
|
|
| ||||||||||
|
Cube-based Geodesic Domes
|
|
|
|
| ||||||||||
|
|
|
|
|
Cuboctahedron-based Geodesic Domes
|
|
|
|
| ||||||||||
|
|
|
|
Truncated Octahedron-based Geodesic Domes
|
|
|
|
|
Rhombicuboctahedron-based Geodesic Domes
|
|
|
|
| ||||||||||
|
Numerical Overview
In order to assist to overview the options further, consider to study following table carefully, it's worth it.- Types: strut types or amount of different strut lengths, the lesser the better
- Variance: strut variance, difference between longest and shortest strut, the lesser the better (more even triangles)
- The L-variant is better than the comperable V-variant, in sense of strut variance and amount of different struts.
The list is sorted by the amount of struts, so you can choose how complex the dome should become.
| Name | Connectors | Faces | Struts | Types | Variance |
 Octahedron 1V Octahedron 1V | 5 | 4 | 8 | 1 | 0% |
 Cube 1V Cube 1V | 10 | 12 | 21 | 2 | 25.6% |
 Icosahedron 1V 2/3 Icosahedron 1V 2/3 | 11 | 15 | 25 | 1 | 0% |
 Cuboctahedron 1V Cuboctahedron 1V | 12 | 16 | 27 | 2 | 30.7% |
 Octahedron 2V Octahedron 2V | 13 | 16 | 28 | 2 | 30.7% |
 Rhombicuboctahedron 1V 3/8 Rhombicuboctahedron 1V 3/8 | 17 | 24 | 40 | 2 | 36.5% |
 Octahedron 3V Octahedron 3V | 25 | 36 | 60 | 3 | 46.1% |
 Octahedron L3 3/8 Octahedron L3 3/8 | 25 | 36 | 60 | 5 | 48.0% |
 Truncated Octahedron 1V Truncated Octahedron 1V | 25 | 36 | 60 | 4 | 46.1% |
 Icosahedron 2V Icosahedron 2V | 26 | 40 | 65 | 2 | 13.1% |
 Cube 2V Cube 2V | 31 | 48 | 78 | 4 | 37.4% |
 Rhombicuboctahedron 1V 5/8 Rhombicuboctahedron 1V 5/8 | 33 | 56 | 88 | 2 | 36.5% |
| Name | Connectors | Faces | Struts | Types | Variance |
 Cuboctahedron 2V Cuboctahedron 2V | 39 | 64 | 102 | 5 | 48.0% |
 Octahedron 4V Octahedron 4V | 41 | 64 | 104 | 6 | 80.2% |
 Octahedron L3 Octahedron L3 | 41 | 64 | 104 | 5 | 48.0% |
 Icosahedron 3V 4/9 Icosahedron 3V 4/9 | 46 | 75 | 120 | 3 | 18.3% |
 Octahedron L3 5/8 Octahedron L3 5/8 | 53 | 92 | 144 | 5 | 48.0% |
 Rhombicuboctahedron 2V 3/8 Rhombicuboctahedron 2V 3/8 | 57 | 96 | 152 | 5 | 44.9% |
 Octahedron 5V Octahedron 5V | 61 | 100 | 160 | 9 | 92.9% |
 Icosahedron 3V 5/9 Icosahedron 3V 5/9 | 61 | 105 | 165 | 3 | 18.3% |
 Cube 3V Cube 3V | 64 | 108 | 171 | 10 | 50.1% |
 Cuboctahedron 3V Cuboctahedron 3V | 82 | 144 | 225 | 10 | 51.2% |
 Octahedron 2V.3V Octahedron 2V.3V | 85 | 144 | 228 | 10 | 51.2% |
 Octahedron 3V.2V Octahedron 3V.2V | 85 | 144 | 228 | 7 | 53.5% |
| Name | Connectors | Faces | Struts | Types | Variance |
 Octahedron 6V Octahedron 6V | 85 | 144 | 228 | 9 | 95.4% |
 Truncated Octahedron 2V Truncated Octahedron 2V | 85 | 144 | 228 | 7 | 53.5% |
 Icosahedron 4V Icosahedron 4V | 91 | 160 | 250 | 6 | 28.3% |
 Icosahedron L3 Icosahedron L3 | 91 | 160 | 250 | 5 | 17.8% |
 Cube 4V Cube 4V | 109 | 192 | 300 | 14 | 56.9% |
 Cube L3 Cube L3 | 109 | 192 | 300 | 11 | 41.5% |
 Octahedron 7V Octahedron 7V | 113 | 196 | 308 | 16 | 107.9% |
 Octahedron L4 7/16 Octahedron L4 7/16 | 113 | 196 | 308 | 15 | 53.8% |
 Rhombicuboctahedron 3V 3/8 Rhombicuboctahedron 3V 3/8 | 121 | 216 | 336 | 10 | 46.2% |
 Rhombicuboctahedron 2V 5/8 Rhombicuboctahedron 2V 5/8 | 121 | 224 | 344 | 5 | 44.9% |
 Icosahedron 5V 7/15 Icosahedron 5V 7/15 | 126 | 225 | 350 | 9 | 32.1% |
 Cuboctahedron 4V Cuboctahedron 4V | 141 | 256 | 396 | 18 | 60.2% |
| Name | Connectors | Faces | Struts | Types | Variance |
 Cuboctahedron L3 Cuboctahedron L3 | 141 | 256 | 396 | 15 | 53.8% |
 Octahedron 8V Octahedron 8V | 145 | 256 | 400 | 20 | 112.6% |
 Octahedron L4 Octahedron L4 | 145 | 256 | 400 | 15 | 53.8% |
 Icosahedron 5V 8/15 Icosahedron 5V 8/15 | 151 | 275 | 425 | 9 | 32.1% |
 Cube 5V Cube 5V | 166 | 300 | 465 | 21 | 58.9% |
 Octahedron L4 9/16 Octahedron L4 9/16 | 173 | 316 | 488 | 15 | 53.8% |
 Octahedron 3V.3V Octahedron 3V.3V | 181 | 324 | 504 | 15 | 55.1% |
 Octahedron 9V Octahedron 9V | 181 | 324 | 504 | 18 | 113.2% |
 Truncated Octahedron 3V Truncated Octahedron 3V | 181 | 324 | 504 | 15 | 55.1% |
 Icosahedron 2V.3V Icosahedron 2V.3V | 196 | 360 | 555 | 10 | 18.9% |
 Icosahedron 6V Icosahedron 6V | 196 | 360 | 555 | 9 | 33.2% |
 Cuboctahedron 5V Cuboctahedron 5V | 216 | 400 | 615 | 28 | 62.8% |
| Name | Connectors | Faces | Struts | Types | Variance |
 Octahedron 10V Octahedron 10V | 221 | 400 | 620 | 30 | 119.3% |
 Octahedron 2V.5V Octahedron 2V.5V | 221 | 400 | 620 | 28 | 62.8% |
 Octahedron 5V.2V Octahedron 5V.2V | 221 | 400 | 620 | 24 | 98.1% |
 Cube 2V.3V Cube 2V.3V | 235 | 432 | 666 | 27 | 44.4% |
 Cube 3V.2V Cube 3V.2V | 235 | 432 | 666 | 22 | 52.3% |
 Cube 6V Cube 6V | 235 | 432 | 666 | 29 | 63.1% |
 Icosahedron 7V 10/21 Icosahedron 7V 10/21 | 246 | 455 | 700 | 15 | 36.5% |
 Rhombicuboctahedron 3V 5/8 Rhombicuboctahedron 3V 5/8 | 265 | 504 | 768 | 10 | 46.2% |
 Icosahedron 7V 11/21 Icosahedron 7V 11/21 | 281 | 525 | 805 | 15 | 36.5% |
 Cuboctahedron 2V.3V Cuboctahedron 2V.3V | 307 | 576 | 882 | 34 | 54.6% |
 Cuboctahedron 3V.2V Cuboctahedron 3V.2V | 307 | 576 | 882 | 28 | 53.6% |
 Cuboctahedron 6V Cuboctahedron 6V | 307 | 576 | 882 | 36 | 63.1% |
| Name | Connectors | Faces | Struts | Types | Variance |
 Truncated Octahedron 4V Truncated Octahedron 4V | 313 | 576 | 888 | 25 | 58.0% |
 Truncated Octahedron L3 Truncated Octahedron L3 | 313 | 576 | 888 | 19 | 55.6% |
 Cube 7V Cube 7V | 316 | 588 | 903 | 42 | 64.0% |
 Icosahedron 8V Icosahedron 8V | 341 | 640 | 980 | 19 | 37.7% |
 Icosahedron L4 Icosahedron L4 | 341 | 640 | 980 | 14 | 19.0% |
Note: all strut lengths have been sorted by 1/10'000th or +/-0.00005 exact
Amount of Struts vs. Strut Variance
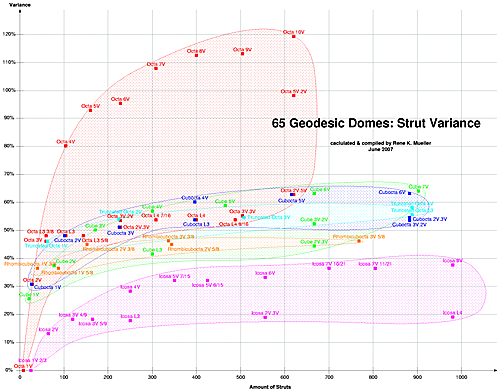  Amount of Struts vs Strut Variance |
Note: Click on the graphic, and click "full scale" or scroll down, and press "Print" link at the bottom of the page.
In the graphic you actually see why the Icosahedron looks best, it has the least strut variance, which is an indication of more or less similiar triangles through the entire structure. And as realized before, the Ln variants additionally provide better results than the nV counterparts. The Octahedron variants, on the other hand, have high strut variances as seen above.
I personally like the Cuboctahedron variants, but they have more strut variance than the Icosahedron, in other words, at the end it's your personal choice and favours which lead you to choose a polyhedral geodesic dome variant, the list above and this graphic may just assist you in your overall considerations.
Amount of Struts vs. Strut Types
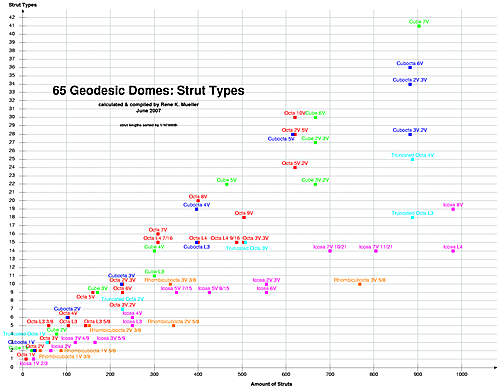  Amount of Struts vs Strut Types |
Note: Click on the graphic, and click "full scale" or scroll down, and press "Print" link at the bottom of the page.
In this graphic above the Icosahedron does quite well, with low amount of strut lengths, and again there also Ln provides better results than the nV variants. Interesting also the Rhombicuboctahedron comes with even lower amount of strut lengths than the Icosahedron.
The amount of different strut lengths has a direct impact on the construction, the lesser the amount of different strut lengths the better - as you have less cut optimization to calculate and therefore less waste to expect.
So it's certainly an aspect to value when choosing a variant to build.
As mentioned already, the struts are sorted in 1/10'000th and you may notice on the details of the variants on the following pages, that you can sum together near the same length struts in case you compose a smaller dome, e.g. < 8m or so.
For large scale domes it may be crucial to remain as precise as you can and I leave it up to you to treat certain struts of alike length as the same or not.
How to Use the Notes
I recommend you choose a dome variant you like to construct ...
- look what base appeals to you most, as a first step disregard any other kind of argument
- check the amount of different strut types, amount of struts itself - and become aware of the overall overhead (e.g. whether building an edgy 1V or 2V, or a smoother 4V or higher with far more struts)
- how temporary shall the dome become? e.g. a 4V Icosahedron Dome skeleton with 250 struts I raise as a single person in 4-5 hours
- the higher the subdivision the more exact you need to work, little difference will distort and weaken the construction
... and once you decided which variant(s) you consider more closely, then ...
- print out that particular page of the dome variant with your settings - as the notes are subject of change, and may later not be available or available with a different notion
- make a 10:1 or 20:1 sized model (e.g. 6m full scale dome, create a 0.60m model), it gives you a sense of the overhead, amount of struts, connectors etc
- think about the kind of strut and its connectors you gonna use, e.g. metal, wood, plastic etc and make tests with the actual material, create a 5-way or 6-way connector construction and test its stability
Strut Options & Notion
For each dome variant there is a small calculator, to calculate diameter to the different struts, additionally the lhole can be entered.
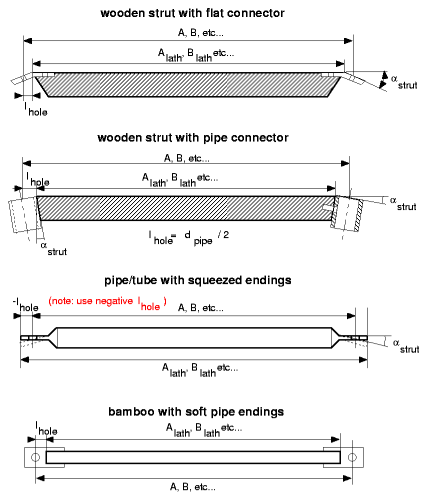 Notion of a dome strut (A vs Alath) & lhole |
Wooden Strut with Flat Connector
Timber based strut, metallic plate as connector, rather cheap with average labour.
Wooden Strut with Pipe Hub
  Pipe Hub Closeup (courtesy by Michal Wielgus) |
Michal Wielgus who sent me the photo used this hub for a 3V 5/9 icosahedron based geodesic dome, he calculated the holes in the pipe for the 5- and 6-way simply by dpipe π / 5 or 6, which was exact enough he said. For the 4-way connectors on the base require the same calculation as the 6-way, and leaving the two bottom directed connectors empty.
To be more precise each hub would require the angles according, A, B, C, etc ...
Following photos were kindly shared by Haan from Korea  , who made a 2V icosahedron based geodesic dome, with 7m diameter, 11cm diameter steel pipe:
, who made a 2V icosahedron based geodesic dome, with 7m diameter, 11cm diameter steel pipe:
Pipe/Tube based Strut
Steel/aluminium/etc tube or pipe, and ends squeezed, also rather cheap with little labour. This options is very popular using conduits.
Desert Domes: Conduit Domes Tips  has some useful information on this option.
has some useful information on this option.
Bamboo Strut
Bamboo (different diameters) with soft-pipe as connector, very cheap but increased labour, and only suitable for small domes < 4-5m diameter and lower sub-division frequencies (e.g. 2V, 3V), e.g. for play domes.
CONBAM.de  , german bamboo expert, has special connectors for more stable and large domes, with a large dome construction
, german bamboo expert, has special connectors for more stable and large domes, with a large dome construction  example.
example.
Bending the Strut-Endings
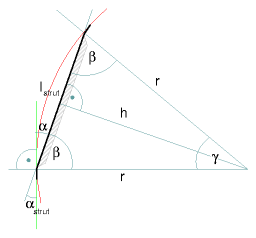 Strut Angle αstrut |
- h = √(r2 - lstrut2/4)
- h = r * cos(γ/2)
- γ = 2 acos(h/r) = 2 acos(√(r2 - lstrut2/4) / r)
- α = 90-&beta
- β = (180-γ)/2
- α = 90 - (180-γ)/2 = γ/2
- α = αstrut = acos(√(r2 - lstrut2/4) / r)
finally α is also the angle to bend the endings αstrut. The following pages with all the variant details provides you for each strut the corresponding αstrut as well.
Detailed Calculation of the Faces or Hub/Strut Angles
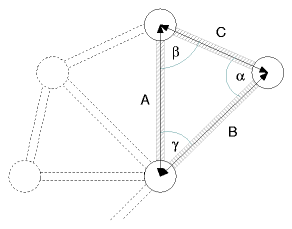 Hub/Strut Angles |
 , known all 3 sides of a triangle searching the angles,
we can calculate all angles:
, known all 3 sides of a triangle searching the angles,
we can calculate all angles:
- α = acos((B2+C2-A2)/(2 B C))
- β = acos((A2+C2-B2)/(2 A C))
- γ = acos((A2+B2-C2)/(2 A B))
For now, all the faces are sorted and the angles are given for all variants.
I may add later a list of hubs and their angles, but you can sort them your based on the construction maps.
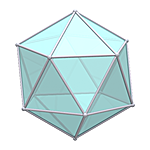
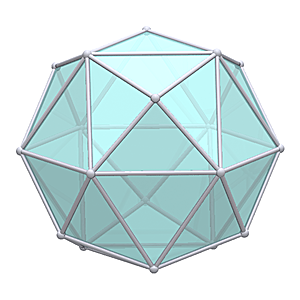
The Icosahedron
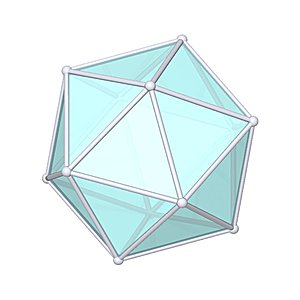  Icosahedron |
- Uniform Polyhedron: U22
- Platonic Solid
- Platonic Element: Water
- Vertices: 12
- Edges: 30
- Faces: 20
- Wythoff symbol: 5|2 3
- Symmetry Group: icosahedral
- Vertex Configuration: {3, 3, 3, 3, 3}
- Dual: dodecahedron
- V: s3 * 5/12 * (3 + √5)
- A: s2 * 20 / 4 * √3
- rinner: s / 12 * (3 * √3 + √15)
- router: s / 4 * √(10 + 2 * √5)
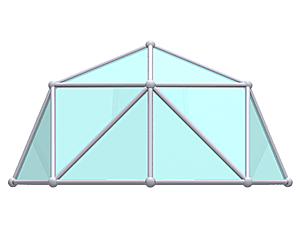
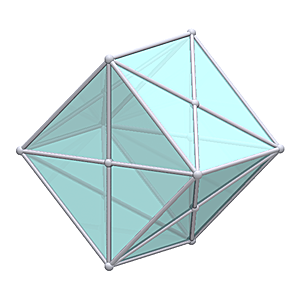
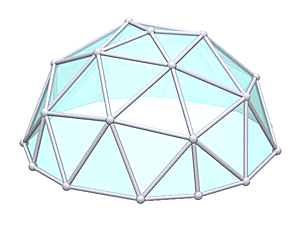
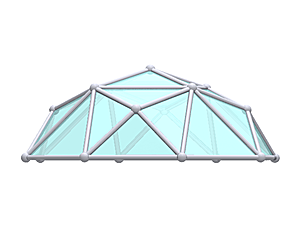
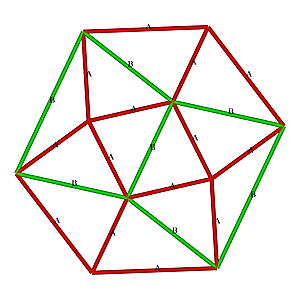
1V/L1 2/3 Icosahedron Dome
|
|
|
- vertices/connectors: 11
- 5 x 4-way
- 6 x 5-way
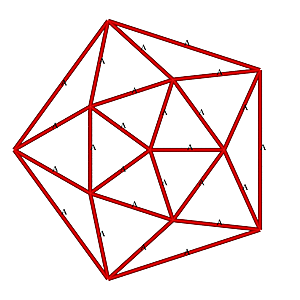
 1V 2/3 Icosahedron Dome Construction Map
1V 2/3 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 25: 1.05146 (31.72°)
- faces: 15 (3-sided)
- A-A-A x 15 (60.00°, 60.00°, 60.00°)
- diameter: 2.000, radius: 1.000
- height: 1.447 or 72.36% of diameter
1V 2/3 Icosahedron Dome Calculator
Geodesic 1V 2/3 Icosahedron Dome (Human is 170cm/5'7") |
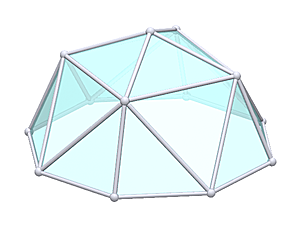
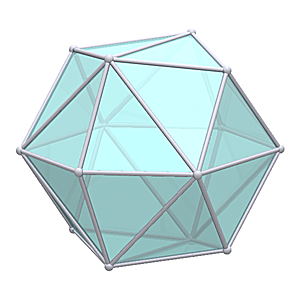
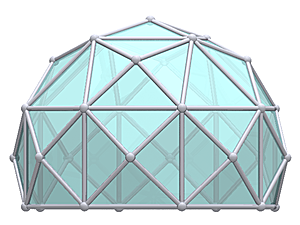
2V/L2 Icosahedron Dome
|
|
|
- vertices/connectors: 26
- 10 x 4-way
- 6 x 5-way
- 10 x 6-way
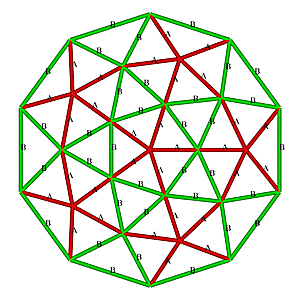
 2V Icosahedron Dome Construction Map
2V Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.54653 (15.86°)
- B x 35: 0.61803 (18.00°)
- total 65 struts (2 kinds)1)
- strut variance 13.1%
- faces: 40 (3-sided)
- A-A-B x 30 (55.57°, 55.57°, 68.86°)
- B-B-B x 10 (60.00°, 60.00°, 60.00°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V Icosahedron Dome Calculator
Geodesic 2V Icosahedron Dome (Human is 170cm/5'7") |
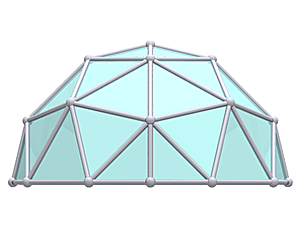
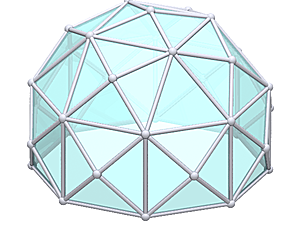
3V 4/9 Icosahedron Dome
In some literature this variant is also called "3V 3/8 Dome".
|
|
|
- vertices/connectors: 46
- 15 x 4-way
- 6 x 5-way
- 25 x 6-way
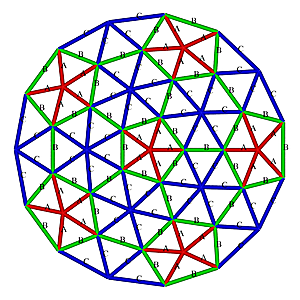
 3V 4/9 Icosahedron Dome Construction Map
3V 4/9 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.34862 (10.04°)
- B x 40: 0.40355 (11.64°)
- C x 50: 0.41241 (11.90°)
- total 120 struts (3 kinds)1)
- strut variance 18.3%
- faces: 75 (3-sided)
- A-A-B x 30 (54.63°, 54.63°, 70.74°)
- B-C-C x 45 (58.59°, 60.70°, 60.70°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.828 or 41.42% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V 4/9 Icosahedron Dome Calculator
Geodesic 3V 4/9 Icosahedron Dome (Human is 170cm/5'7") |
As you see the bottom isn't entirely even, for heavy construction you have to level them.
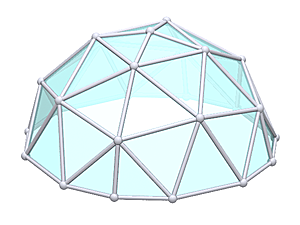
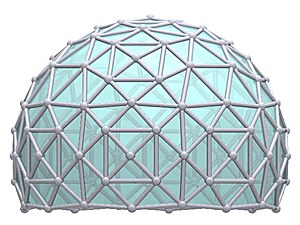
3V 5/9 Icosahedron Dome
In some literature this variant is also called "3V 5/8 Dome".
|
|
|
- vertices/connectors: 61
- 15 x 4-way
- 6 x 5-way
- 40 x 6-way
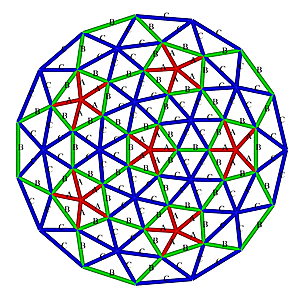
 3V 5/9 Icosahedron Dome Construction Map
3V 5/9 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.34862 (10.04°)
- B x 55: 0.40355 (11.64°)
- C x 80: 0.41241 (11.90°)
- total 165 struts (3 kinds)1)
- strut variance 18.3%
- faces: 105 (3-sided)
- A-A-B x 30 (54.63°, 54.63°, 70.74°)
- B-C-C x 75 (58.59°, 60.70°, 60.70°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.188 or 59.38% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V 5/9 Icosahedron Dome Calculator
Geodesic 3V 5/9 Icosahedron Dome (Human is 170cm/5'7") |
As you see here as well that the bottom isn't entirely even, for heavy construction you have to level them.
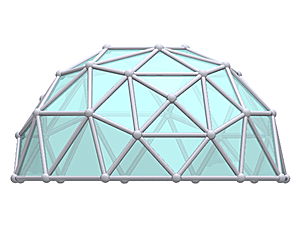
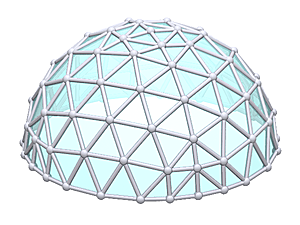
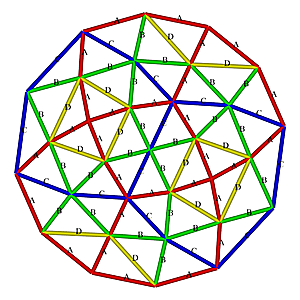
4V Icosahedron Dome
|
|
|
- vertices/connectors: 91
- 20 x 4-way
- 6 x 5-way
- 65 x 6-way
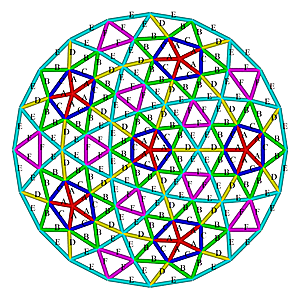
 4V Icosahedron Dome Construction Map
4V Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.25318 (7.27°)
- B x 60: 0.29453 (8.47°)
- C x 30: 0.29524 (8.49°)
- D x 30: 0.29859 (8.59°)
- E x 70: 0.31287 (9.00°)
- F x 30: 0.32492 (9.35°)
- total 250 struts (6 kinds)1)
- strut variance 28.3%
- faces: 160 (3-sided)
- A-A-C x 30 (54.34°, 54.34°, 71.32°)
- B-B-C x 30 (59.92°, 59.92°, 60.16°)
- B-D-E x 60 (57.52°, 58.80°, 63.68°)
- E-E-F x 30 (58.72°, 58.72°, 62.55°)
- F-F-F x 10 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
4V Icosahedron Dome Calculator
Geodesic 4V Icosahedron Dome (Human is 170cm/5'7") |
The 4V looks very attractive, yet, I would recommend using the L3 version instead with less strut lengths and less strut variance.
L3 Icosahedron Dome
|
|
|
- vertices/connectors: 91
- 20 x 4-way
- 6 x 5-way
- 65 x 6-way
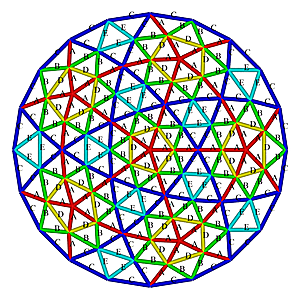
 L3 Icosahedron Dome Construction Map
L3 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 60: 0.27590 (7.93°)
- B x 60: 0.28547 (8.21°)
- C x 70: 0.31287 (9.00°)
- D x 30: 0.32124 (9.24°)
- E x 30: 0.32492 (9.35°)
- total 250 struts (5 kinds)1)
- strut variance 17.8%
- faces: 160 (3-sided)
- A-A-D x 30 (54.40°, 54.40°, 71.20°)
- A-B-C x 60 (54.68°, 57.60°, 67.72°)
- B-B-D x 30 (55.77°, 55.77°, 68.46°)
- C-C-E x 30 (58.72°, 58.72°, 62.55°)
- E-E-E x 10 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 Icosahedron Dome Calculator
Geodesic L3 Icosahedron Dome (Human is 170cm/5'7") |
The L3 might be a better choice for a 250 strut dome than the 4V variant: the L3 provides less strut variance 17.8% (5 kinds of struts) instead of 28.3% (6 kinds of struts).
5V 7/15 Icosahedron Dome
|
|
|
- vertices/connectors: 126
- 25 x 4-way
- 6 x 5-way
- 95 x 6-way
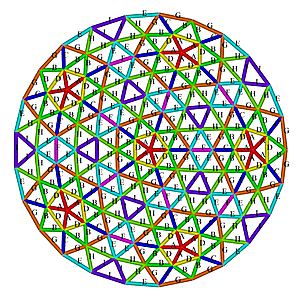
 5V 7/15 Icosahedron Dome Construction Map
5V 7/15 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.19815 (5.69°)
- B x 60: 0.22569 (6.48°)
- C x 30: 0.23160 (6.65°)
- D x 30: 0.23179 (6.66°)
- E x 50: 0.24509 (7.04°)
- F x 10: 0.24535 (7.05°)
- G x 60: 0.24724 (7.10°)
- H x 50: 0.25517 (7.33°)
- I x 30: 0.26160 (7.52°)
- total 350 struts (9 kinds)1)
- strut variance 32.1%
- faces: 225 (3-sided)
- A-A-D x 30 (54.19°, 54.19°, 71.61°)
- B-B-D x 30 (59.10°, 59.10°, 61.80°)
- B-C-G x 60 (56.13°, 58.44°, 65.43°)
- E-E-F x 20 (59.96°, 59.96°, 60.08°)
- E-G-H x 50 (58.37°, 59.18°, 62.45°)
- H-H-I x 25 (59.17°, 59.17°, 61.67°)
- I-I-I x 10 (60.00°, 60.00°, 60.00°)
- 7 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.896 or 44.78% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V 7/15 Icosahedron Dome Calculator
Geodesic 5V 7/15 Icosahedron Dome (Human is 170cm/5'7") |
5V 8/15 Icosahedron Dome
|
|
|
- vertices/connectors: 151
- 25 x 4-way
- 6 x 5-way
- 120 x 6-way
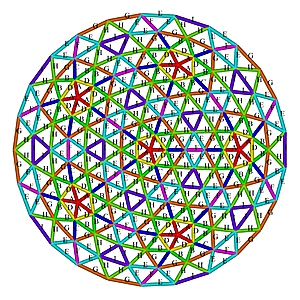
 5V 8/15 Icosahedron Dome Construction Map
5V 8/15 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.19815 (5.69°)
- B x 60: 0.22569 (6.48°)
- C x 30: 0.23160 (6.65°)
- D x 30: 0.23179 (6.66°)
- E x 80: 0.24509 (7.04°)
- F x 20: 0.24535 (7.05°)
- G x 70: 0.24724 (7.10°)
- H x 70: 0.25517 (7.33°)
- I x 35: 0.26160 (7.52°)
- total 425 struts (9 kinds)1)
- strut variance 32.1%
- faces: 275 (3-sided)
- A-A-D x 30 (54.19°, 54.19°, 71.61°)
- B-B-D x 30 (59.10°, 59.10°, 61.80°)
- B-C-G x 60 (56.13°, 58.44°, 65.43°)
- E-E-F x 40 (59.96°, 59.96°, 60.08°)
- E-G-H x 70 (58.37°, 59.18°, 62.45°)
- H-H-I x 35 (59.17°, 59.17°, 61.67°)
- I-I-I x 10 (60.00°, 60.00°, 60.00°)
- 7 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.111 or 55.56% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V 8/15 Icosahedron Dome Calculator
Geodesic 5V 8/15 Icosahedron Dome (Human is 170cm/5'7") |
6V Icosahedron Dome
|
|
|
- vertices/connectors: 196
- 30 x 4-way
- 6 x 5-way
- 160 x 6-way
 6V Icosahedron Dome Construction Map
6V Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.16257 (4.66°)
- B x 60: 0.18191 (5.22°)
- C x 30: 0.18738 (5.38°)
- D x 30: 0.19048 (5.47°)
- E x 60: 0.19801 (5.68°)
- F x 90: 0.20282 (5.82°)
- G x 130: 0.20591 (5.91°)
- H x 65: 0.21535 (6.18°)
- I x 60: 0.21663 (6.22°)
- total 555 struts (9 kinds)1)
- strut variance 33.2%
- faces: 360 (3-sided)
- A-A-D x 30 (54.14°, 54.14°, 71.72°)
- B-B-D x 30 (58.42°, 58.42°, 63.15°)
- B-C-F x 60 (55.40°, 58.00°, 66.60°)
- E-F-G x 120 (57.95°, 60.24°, 61.81°)
- G-G-H x 60 (58.46°, 58.46°, 63.08°)
- H-I-I x 60 (59.63°, 60.18°, 60.18°)
- 6 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
6V Icosahedron Dome Calculator
Geodesic 6V Icosahedron Dome (Human is 170cm/5'7") |
2V.3V Icosahedron Dome
|
|
|
- vertices/connectors: 196
- 30 x 4-way
- 6 x 5-way
- 160 x 6-way
 2V.3V Icosahedron Dome Construction Map
2V.3V Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 60: 0.18212 (5.22°)
- B x 30: 0.18854 (5.41°)
- C x 60: 0.18922 (5.43°)
- D x 60: 0.18932 (5.43°)
- E x 60: 0.19125 (5.49°)
- F x 70: 0.20591 (5.91°)
- G x 30: 0.21321 (6.12°)
- H x 60: 0.21445 (6.16°)
- I x 65: 0.21535 (6.18°)
- J x 60: 0.21663 (6.22°)
- total 555 struts (10 kinds)1)
- strut variance 18.9%
- faces: 360 (3-sided)
- A-A-G x 30 (54.17°, 54.17°, 71.66°)
- A-C-F x 60 (54.69°, 57.98°, 67.33°)
- B-D-H x 60 (55.23°, 55.58°, 69.19°)
- C-E-H x 60 (55.22°, 56.15°, 68.63°)
- D-D-G x 30 (55.73°, 55.73°, 68.54°)
- E-E-I x 30 (55.74°, 55.74°, 68.53°)
- F-F-I x 30 (58.46°, 58.46°, 63.08°)
- I-J-J x 60 (59.63°, 60.18°, 60.18°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V.3V Icosahedron Dome Calculator
Geodesic 2V.3V Icosahedron Dome (Human is 170cm/5'7") |
The 2V.3V has 10 kinds of strut lengths, and 18.7% strut variance - compared to 6V with 9 kinds and 33.3% variance. So, you might think about prefering more even triangles, choose 2V.3V or less struth kinds then the 6V.
3V.2V Icosahedron Dome
The 3V.2V Icosahedron could also be used to achieve the same amount of subdivision, yet, the 3V is a bit uneven around the base, and the 2nd stage of 2V doesn't even this again, so the base isn't even, yet, 7 kinds of struts. I won't list the details as I won't recommend 3V.2V over 2V.3V or 6V at all.7V 10/21 Icosahedron Dome
|
|
|
- vertices/connectors: 246
- 35 x 4-way
- 6 x 5-way
- 205 x 6-way
 7V 10/21 Icosahedron Dome Construction Map
7V 10/21 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.13774 (3.95°)
- B x 60: 0.15197 (4.36°)
- C x 30: 0.15664 (4.49°)
- D x 30: 0.16154 (4.63°)
- E x 60: 0.16480 (4.73°)
- F x 30: 0.17066 (4.90°)
- G x 60: 0.17098 (4.90°)
- H x 60: 0.17132 (4.91°)
- I x 50: 0.17353 (4.98°)
- J x 70: 0.17585 (5.04°)
- K x 50: 0.18155 (5.21°)
- L x 30: 0.18161 (5.21°)
- M x 50: 0.18237 (5.23°)
- N x 60: 0.18548 (5.32°)
- O x 30: 0.18791 (5.39°)
- total 700 struts (15 kinds)1)
- strut variance 36.5%
- faces: 455 (3-sided)
- A-A-D x 30 (54.10°, 54.10°, 71.81°)
- B-B-D x 30 (57.91°, 57.91°, 64.18°)
- B-C-H x 60 (55.01°, 57.57°, 67.41°)
- E-F-J x 60 (56.76°, 60.03°, 63.21°)
- E-G-H x 60 (57.56°, 61.13°, 61.31°)
- G-G-L x 30 (57.93°, 57.93°, 64.15°)
- I-I-J x 20 (59.54°, 59.54°, 60.92°)
- I-J-M x 50 (57.89°, 59.18°, 62.93°)
- K-K-L x 25 (59.98°, 59.98°, 60.04°)
- K-M-N x 50 (59.11°, 59.59°, 61.29°)
- N-N-O x 30 (59.57°, 59.57°, 60.86°)
- O-O-O x 10 (60.00°, 60.00°, 60.00°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.925 or 46.26% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
7V 10/21 Icosahedron Dome Calculator
Geodesic 7V 10/21 Icosahedron Dome (Human is 170cm/5'7") |
7V 11/21 Icosahedron Dome
|
|
|
- vertices/connectors: 281
- 35 x 4-way
- 6 x 5-way
- 240 x 6-way
 7V 11/21 Icosahedron Dome Construction Map
7V 11/21 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.13774 (3.95°)
- B x 60: 0.15197 (4.36°)
- C x 30: 0.15664 (4.49°)
- D x 30: 0.16154 (4.63°)
- E x 60: 0.16480 (4.73°)
- F x 30: 0.17066 (4.90°)
- G x 60: 0.17098 (4.90°)
- H x 60: 0.17132 (4.91°)
- I x 80: 0.17353 (4.98°)
- J x 90: 0.17585 (5.04°)
- K x 70: 0.18155 (5.21°)
- L x 35: 0.18161 (5.21°)
- M x 70: 0.18237 (5.23°)
- N x 70: 0.18548 (5.32°)
- O x 30: 0.18791 (5.39°)
- total 805 struts (15 kinds)1)
- strut variance 36.5%
- faces: 525 (3-sided)
- A-A-D x 30 (54.10°, 54.10°, 71.81°)
- B-B-D x 30 (57.91°, 57.91°, 64.18°)
- B-C-H x 60 (55.01°, 57.57°, 67.41°)
- E-F-J x 60 (56.76°, 60.03°, 63.21°)
- E-G-H x 60 (57.56°, 61.13°, 61.31°)
- G-G-L x 30 (57.93°, 57.93°, 64.15°)
- I-I-J x 40 (59.54°, 59.54°, 60.92°)
- I-J-M x 70 (57.89°, 59.18°, 62.93°)
- K-K-L x 35 (59.98°, 59.98°, 60.04°)
- K-M-N x 70 (59.11°, 59.59°, 61.29°)
- N-N-O x 30 (59.57°, 59.57°, 60.86°)
- O-O-O x 10 (60.00°, 60.00°, 60.00°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.080 or 54.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
7V 11/21 Icosahedron Dome Calculator
Geodesic 7V 11/21 Icosahedron Dome (Human is 170cm/5'7") |
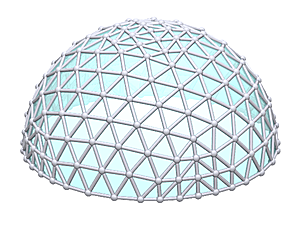
8V Icosahedron Dome
|
|
|
- vertices/connectors: 341
- 40 x 4-way
- 6 x 5-way
- 295 x 6-way
 8V Icosahedron Dome Construction Map
8V Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 30: 0.11946 (3.42°)
- B x 60: 0.13033 (3.74°)
- C x 30: 0.13424 (3.85°)
- D x 30: 0.14018 (4.02°)
- E x 60: 0.14056 (4.03°)
- F x 60: 0.14548 (4.17°)
- G x 30: 0.14628 (4.19°)
- H x 60: 0.14803 (4.24°)
- I x 60: 0.14862 (4.26°)
- J x 60: 0.15267 (4.38°)
- K x 70: 0.15296 (4.39°)
- L x 30: 0.15315 (4.39°)
- M x 60: 0.15477 (4.44°)
- N x 90: 0.15636 (4.48°)
- O x 60: 0.16033 (4.60°)
- P x 30: 0.16036 (4.60°)
- Q x 70: 0.16088 (4.61°)
- R x 60: 0.16300 (4.67°)
- S x 30: 0.16465 (4.72°)
- total 980 struts (19 kinds)1)
- strut variance 37.7%
- faces: 640 (3-sided)
- A-A-D x 30 (54.08°, 54.08°, 71.83°)
- B-B-D x 30 (57.45°, 57.45°, 65.09°)
- B-C-H x 60 (54.73°, 57.24°, 68.03°)
- E-F-H x 60 (57.24°, 60.49°, 62.28°)
- E-G-J x 60 (56.05°, 59.67°, 64.28°)
- F-F-N x 30 (57.49°, 57.49°, 65.02°)
- I-J-N x 60 (57.45°, 60.02°, 62.52°)
- I-K-L x 60 (58.06°, 60.90°, 61.04°)
- K-K-P x 30 (58.39°, 58.39°, 63.23°)
- M-M-N x 30 (59.66°, 59.66°, 60.69°)
- M-N-Q x 60 (58.38°, 59.36°, 62.26°)
- O-O-P x 30 (59.98°, 59.98°, 60.04°)
- O-Q-R x 60 (59.32°, 59.69°, 60.99°)
- R-R-S x 30 (59.67°, 59.67°, 60.65°)
- S-S-S x 10 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
8V Icosahedron Dome Calculator
Geodesic 8V Icosahedron Dome (Human is 170cm/5'7") |
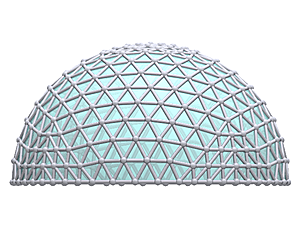
L4 Icosahedron Dome
|
|
|
- vertices/connectors: 341
- 40 x 4-way
- 6 x 5-way
- 295 x 6-way
 L4 Icosahedron Dome Construction Map
L4 Icosahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 120: 0.13828 (3.96°)
- B x 120: 0.13951 (4.00°)
- C x 120: 0.14310 (4.10°)
- D x 60: 0.14429 (4.14°)
- E x 60: 0.14439 (4.14°)
- F x 140: 0.15692 (4.50°)
- G x 60: 0.15800 (4.53°)
- H x 60: 0.15846 (4.54°)
- I x 60: 0.16115 (4.62°)
- J x 30: 0.16217 (4.65°)
- K x 30: 0.16228 (4.65°)
- L x 60: 0.16300 (4.67°)
- M x 30: 0.16448 (4.72°)
- N x 30: 0.16465 (4.72°)
- total 980 struts (14 kinds)1)
- strut variance 19.0%
- faces: 640 (3-sided)
- A-A-J x 30 (54.10°, 54.10°, 71.80°)
- A-B-I x 60 (54.21°, 54.90°, 70.89°)
- A-C-G x 60 (54.41°, 57.29°, 68.29°)
- A-D-F x 60 (54.47°, 58.12°, 67.41°)
- B-B-J x 30 (54.45°, 54.45°, 71.09°)
- B-C-F x 60 (55.19°, 57.38°, 67.44°)
- B-D-G x 60 (54.74°, 57.63°, 67.64°)
- C-C-K x 30 (55.45°, 55.45°, 69.09°)
- C-E-I x 60 (55.54°, 56.30°, 68.16°)
- E-E-K x 30 (55.81°, 55.81°, 68.39°)
- F-F-M x 30 (58.38°, 58.38°, 63.23°)
- F-H-L x 60 (58.40°, 59.36°, 62.23°)
- H-H-M x 30 (58.74°, 58.74°, 62.52°)
- L-L-N x 30 (59.67°, 59.67°, 60.65°)
- N-N-N x 10 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L4 Icosahedron Dome Calculator
Geodesic L4 Icosahedron Dome (Human is 170cm/5'7") |
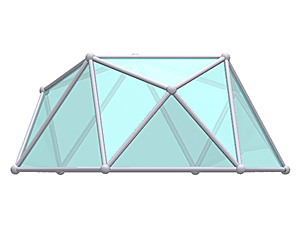
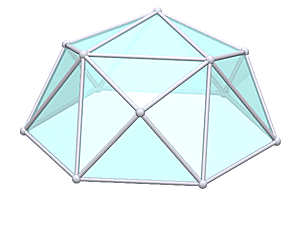
The Octahedron
  Octahedron |
- Uniform Polyhedron: U5
- Platonic Solid
- Platonic Element: Air
- Vertices: 6
- Edges: 12
- Faces: 8
- Wythoff symbol: 4|2 3
- Symmetry Group: octahedral
- Vertex Configuration: {3, 3, 3, 3}
- Dual: cube
- V: s3 / 3 * √2
- A: s2 * 8 / 4 * √3
- rinner: s / 6 * √6
- router: s / 2 * √2
1V/L1 Octahedron Dome
|
|
|
- vertices/connectors: 5
- 4 x 3-way
- 1 x 4-way
 1V Octahedron Dome Construction Map
1V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 8: 1.41421 (45.00°)
- faces: 4 (3-sided)
- A-A-A x 4 (60.00°, 60.00°, 60.00°)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1V Octahedron Dome Calculator
Geodesic 1V Octahedron Dome (Human is 170cm/5'7") |
2V/L2 Octahedron Dome
|
|
|
- vertices/connectors: 13
- 4 x 3-way
- 5 x 4-way
- 4 x 6-way
 2V Octahedron Dome Construction Map
2V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.76537 (22.50°)
- B x 12: 1.00000 (30.00°)
- total 28 struts (2 kinds)1)
- strut variance 30.7%
- faces: 16 (3-sided)
- A-A-B x 12 (49.21°, 49.21°, 81.57°)
- B-B-B x 4 (60.00°, 60.00°, 60.00°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V Octahedron Dome Calculator
Geodesic 2V Octahedron Dome (Human is 170cm/5'7") |
3V Octahedron Dome
|
|
|
- vertices/connectors: 25
- 4 x 3-way
- 9 x 4-way
- 12 x 6-way
 3V Octahedron Dome Construction Map
3V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.45951 (13.28°)
- B x 20: 0.63246 (18.44°)
- C x 24: 0.67142 (19.62°)
- total 60 struts (3 kinds)1)
- strut variance 46.1%
- faces: 36 (3-sided)
- A-A-B x 12 (46.51°, 46.51°, 86.98°)
- B-C-C x 24 (56.20°, 61.90°, 61.90°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V Octahedron Dome Calculator
Geodesic 3V Octahedron Dome (Human is 170cm/5'7") |
4V Octahedron Dome
|
|
|
- vertices/connectors: 41
- 4 x 3-way
- 13 x 4-way
- 24 x 6-way
 4V Octahedron Dome Construction Map
4V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.32036 (9.22°)
- B x 24: 0.43887 (12.68°)
- C x 12: 0.44721 (12.92°)
- D x 16: 0.45951 (13.28°)
- E x 24: 0.51764 (15.00°)
- F x 12: 0.57735 (16.78°)
- total 104 struts (6 kinds)1)
- strut variance 80.2%
- faces: 64 (3-sided)
- A-A-C x 12 (45.74°, 45.74°, 88.51°)
- B-B-C x 12 (59.37°, 59.37°, 61.26°)
- B-D-E x 24 (52.98°, 56.71°, 70.32°)
- E-E-F x 12 (56.10°, 56.10°, 67.80°)
- F-F-F x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
4V Octahedron Dome Calculator
Geodesic 4V Octahedron Dome (Human is 170cm/5'7") |
L3 Octahedron Dome
|
|
|
- vertices/connectors: 41
- 4 x 3-way
- 13 x 4-way
- 24 x 6-way
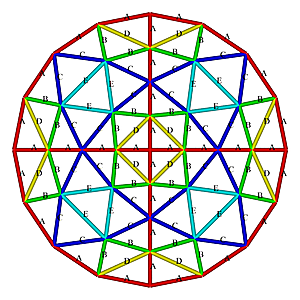
 L3 Octahedron Dome Construction Map
L3 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.39018 (11.25°)
- B x 24: 0.42291 (12.21°)
- C x 24: 0.51764 (15.00°)
- D x 12: 0.54120 (15.70°)
- E x 12: 0.57735 (16.78°)
- total 104 struts (5 kinds)1)
- strut variance 48.0%
- faces: 64 (3-sided)
- A-A-D x 12 (46.09°, 46.09°, 87.81°)
- A-B-C x 24 (47.72°, 53.31°, 78.96°)
- B-B-D x 12 (50.22°, 50.22°, 79.56°)
- C-C-E x 12 (56.10°, 56.10°, 67.80°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 Octahedron Dome Calculator
Geodesic L3 Octahedron Dome (Human is 170cm/5'7") |
The nice thing is here, that the L3 provides at 3/8 and 5/8 also an almost even base line.
L3 1/4 Octahedron Dome
|
|
|
- vertices/connectors: 25
- 4 x 3-way
- 9 x 4-way
- 12 x 6-way
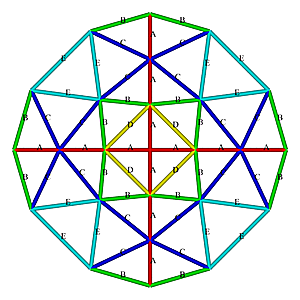
 L3 3/8 Octahedron Dome Construction Map
L3 3/8 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 12: 0.39018 (11.25°)
- B x 16: 0.42291 (12.21°)
- C x 16: 0.51764 (15.00°)
- D x 4: 0.54120 (15.70°)
- E x 12: 0.57735 (16.78°)
- total 60 struts (5 kinds)1)
- strut variance 48.0%
- faces: 36 (3-sided)
- A-A-D x 4 (46.09°, 46.09°, 87.81°)
- A-B-C x 16 (47.72°, 53.31°, 78.96°)
- B-B-D x 4 (50.22°, 50.22°, 79.56°)
- C-C-E x 8 (56.10°, 56.10°, 67.80°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.617 or 30.87% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 3/8 Octahedron Dome Calculator
Geodesic L3 3/8 Octahedron Dome (Human is 170cm/5'7") |
Here again uneven base, for heavy construction leveling necessary.
L3 5/8 Octahedron Dome
|
|
|
- vertices/connectors: 53
- 13 x 4-way
- 4 x 5-way
- 36 x 6-way
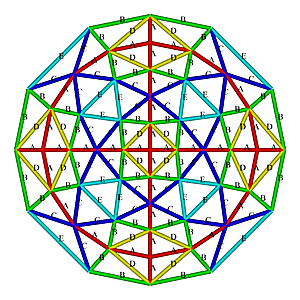
 L3 5/8 Octahedron Dome Construction Map
L3 5/8 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 36: 0.39018 (11.25°)
- B x 40: 0.42291 (12.21°)
- C x 32: 0.51764 (15.00°)
- D x 20: 0.54120 (15.70°)
- E x 16: 0.57735 (16.78°)
- total 144 struts (5 kinds)1)
- strut variance 48.0%
- faces: 92 (3-sided)
- A-A-D x 20 (46.09°, 46.09°, 87.81°)
- A-B-C x 32 (47.72°, 53.31°, 78.96°)
- B-B-D x 20 (50.22°, 50.22°, 79.56°)
- C-C-E x 16 (56.10°, 56.10°, 67.80°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.408 or 70.41% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 5/8 Octahedron Dome Calculator
Geodesic L3 5/8 Octahedron Dome (Human is 170cm/5'7") |
Here again uneven base, for heavy construction leveling necessary.
5V Octahedron Dome
|
|
|
- vertices/connectors: 61
- 4 x 3-way
- 17 x 4-way
- 40 x 6-way
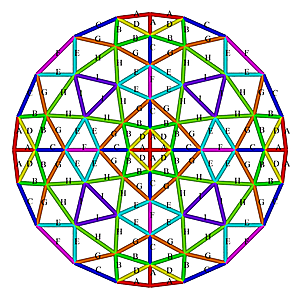
 5V Octahedron Dome Construction Map
5V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.24437 (7.02°)
- B x 24: 0.31415 (9.04°)
- C x 16: 0.34134 (9.83°)
- D x 12: 0.34300 (9.88°)
- E x 24: 0.38859 (11.20°)
- F x 8: 0.39223 (11.31°)
- G x 24: 0.40033 (11.55°)
- H x 24: 0.43696 (12.62°)
- I x 12: 0.47140 (13.63°)
- total 160 struts (9 kinds)1)
- strut variance 92.9%
- faces: 100 (3-sided)
- A-A-D x 12 (45.43°, 45.43°, 89.13°)
- B-B-D x 12 (56.91°, 56.91°, 66.19°)
- B-C-G x 24 (49.33°, 55.51°, 75.16°)
- E-E-F x 12 (59.69°, 59.69°, 60.61°)
- E-G-H x 24 (55.09°, 57.65°, 67.26°)
- H-H-I x 12 (57.36°, 57.36°, 65.28°)
- I-I-I x 4 (60.00°, 60.00°, 60.00°)
- 7 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V Octahedron Dome Calculator
Geodesic 5V Octahedron Dome (Human is 170cm/5'7") |
6V Octahedron Dome
|
|
|
- vertices/connectors: 85
- 4 x 3-way
- 21 x 4-way
- 60 x 6-way
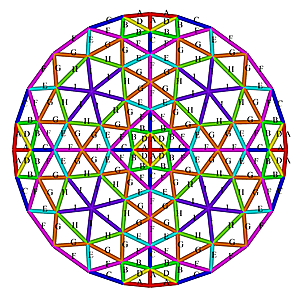
 6V Octahedron Dome Construction Map
6V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.19708 (5.66°)
- B x 24: 0.24197 (6.95°)
- C x 16: 0.26547 (7.63°)
- D x 12: 0.27735 (7.97°)
- E x 24: 0.29603 (8.51°)
- F x 40: 0.32036 (9.22°)
- G x 48: 0.33193 (9.55°)
- H x 24: 0.37796 (10.89°)
- I x 24: 0.38518 (11.10°)
- total 228 struts (9 kinds)1)
- strut variance 95.4%
- faces: 144 (3-sided)
- A-A-D x 12 (45.30°, 45.30°, 89.41°)
- B-B-D x 12 (55.04°, 55.04°, 69.91°)
- B-C-F x 24 (47.66°, 54.19°, 78.15°)
- E-F-G x 48 (53.94°, 61.05°, 65.02°)
- G-G-H x 24 (55.29°, 55.29°, 69.42°)
- H-I-I x 24 (58.77°, 60.62°, 60.62°)
- 6 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
6V Octahedron Dome Calculator
Geodesic 6V Octahedron Dome (Human is 170cm/5'7") |
2V.3V Octahedron Dome
|
|
|
- vertices/connectors: 85
- 4 x 3-way
- 21 x 4-way
- 60 x 6-way
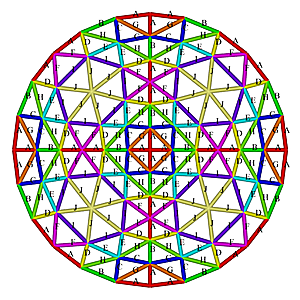
 2V.3V Octahedron Dome Construction Map
2V.3V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.25480 (7.32°)
- B x 16: 0.27355 (7.86°)
- C x 24: 0.27468 (7.89°)
- D x 24: 0.27569 (7.92°)
- E x 24: 0.29082 (8.36°)
- F x 24: 0.33193 (9.55°)
- G x 12: 0.35741 (10.29°)
- H x 24: 0.36346 (10.47°)
- I x 24: 0.37796 (10.89°)
- J x 24: 0.38518 (11.10°)
- total 228 struts (10 kinds)1)
- strut variance 51.2%
- faces: 144 (3-sided)
- A-A-G x 12 (45.47°, 45.47°, 89.07°)
- A-D-F x 24 (48.51°, 54.14°, 77.35°)
- B-C-H x 24 (48.34°, 48.60°, 83.05°)
- C-C-G x 12 (49.42°, 49.42°, 81.16°)
- D-E-H x 24 (48.28°, 51.94°, 79.78°)
- E-E-I x 12 (49.46°, 49.46°, 81.07°)
- F-F-I x 12 (55.29°, 55.29°, 69.42°)
- I-J-J x 24 (58.77°, 60.62°, 60.62°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V.3V Octahedron Dome Calculator
Geodesic 2V.3V Octahedron Dome (Human is 170cm/5'7") |
3V.2V Octahedron Dome
|
|
|
- vertices/connectors: 85
- 4 x 3-way
- 21 x 4-way
- 60 x 6-way
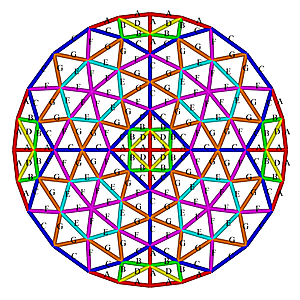
 3V.2V Octahedron Dome Construction Map
3V.2V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.23131 (6.64°)
- B x 24: 0.23773 (6.83°)
- C x 40: 0.32036 (9.22°)
- D x 12: 0.32492 (9.35°)
- E x 24: 0.33571 (9.66°)
- F x 48: 0.34069 (9.81°)
- G x 48: 0.35506 (10.23°)
- total 228 struts (7 kinds)1)
- strut variance 53.5%
- faces: 144 (3-sided)
- A-A-D x 12 (45.39°, 45.39°, 89.23°)
- A-B-C x 24 (46.08°, 47.75°, 86.17°)
- B-B-D x 12 (46.89°, 46.89°, 86.22°)
- C-F-G x 48 (54.79°, 60.32°, 64.89°)
- E-F-F x 24 (59.03°, 60.48°, 60.48°)
- E-G-G x 24 (56.42°, 61.79°, 61.79°)
- 6 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V.2V Octahedron Dome Calculator
Geodesic 3V.2V Octahedron Dome (Human is 170cm/5'7") |
7V Octahedron Dome
|
|
|
- vertices/connectors: 113
- 4 x 3-way
- 25 x 4-way
- 84 x 6-way
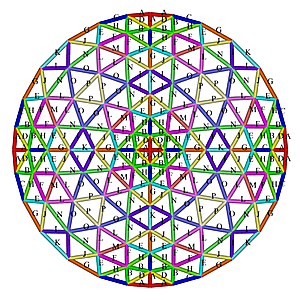
 7V Octahedron Dome Construction Map
7V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.16496 (4.73°)
- B x 24: 0.19598 (5.62°)
- C x 16: 0.21494 (6.17°)
- D x 12: 0.23250 (6.68°)
- E x 24: 0.23440 (6.73°)
- F x 24: 0.26112 (7.50°)
- G x 16: 0.26224 (7.53°)
- H x 24: 0.26495 (7.61°)
- I x 24: 0.27001 (7.76°)
- J x 24: 0.28228 (8.11°)
- K x 8: 0.28284 (8.13°)
- L x 24: 0.30770 (8.85°)
- M x 12: 0.30861 (8.88°)
- N x 24: 0.31244 (8.99°)
- O x 24: 0.32892 (9.47°)
- P x 12: 0.34300 (9.88°)
- total 308 struts (16 kinds)1)
- strut variance 107.9%
- faces: 196 (3-sided)
- A-A-D x 12 (45.21°, 45.21°, 89.59°)
- B-B-D x 12 (53.62°, 53.62°, 72.76°)
- B-C-H x 24 (46.78°, 53.04°, 80.18°)
- E-F-H x 24 (52.91°, 62.69°, 64.40°)
- E-G-J x 24 (50.83°, 60.14°, 69.03°)
- F-F-M x 12 (53.77°, 53.77°, 72.45°)
- I-I-K x 12 (58.42°, 58.42°, 63.16°)
- I-J-N x 24 (53.71°, 57.44°, 68.85°)
- L-L-M x 12 (59.90°, 59.90°, 60.19°)
- L-N-O x 24 (57.28°, 58.66°, 64.06°)
- O-O-P x 12 (58.57°, 58.57°, 62.86°)
- P-P-P x 4 (60.00°, 60.00°, 60.00°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
7V Octahedron Dome Calculator
Geodesic 7V Octahedron Dome (Human is 170cm/5'7") |
8V Octahedron Dome
|
|
|
- vertices/connectors: 145
- 4 x 3-way
- 29 x 4-way
- 112 x 6-way
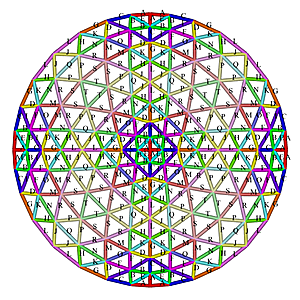
 8V Octahedron Dome Construction Map
8V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.14178 (4.07°)
- B x 24: 0.16439 (4.71°)
- C x 16: 0.17961 (5.15°)
- D x 24: 0.19238 (5.52°)
- E x 12: 0.20000 (5.74°)
- F x 24: 0.21272 (6.11°)
- G x 16: 0.21823 (6.26°)
- H x 24: 0.22192 (6.37°)
- I x 24: 0.22504 (6.46°)
- J x 24: 0.24197 (6.95°)
- K x 24: 0.24229 (6.96°)
- L x 16: 0.24437 (7.02°)
- M x 24: 0.24915 (7.16°)
- N x 24: 0.25786 (7.41°)
- O x 12: 0.25820 (7.42°)
- P x 24: 0.27685 (7.96°)
- Q x 12: 0.27735 (7.97°)
- R x 24: 0.28011 (8.05°)
- S x 24: 0.29180 (8.39°)
- T x 12: 0.30151 (8.67°)
- total 400 struts (20 kinds)1)
- strut variance 112.6%
- faces: 256 (3-sided)
- A-A-E x 12 (45.15°, 45.15°, 89.69°)
- B-B-E x 12 (52.54°, 52.54°, 74.93°)
- B-C-I x 24 (46.28°, 52.15°, 81.57°)
- D-F-I x 24 (52.06°, 60.68°, 67.26°)
- D-G-K x 24 (49.05°, 58.93°, 72.02°)
- F-F-O x 12 (52.63°, 52.63°, 74.74°)
- H-J-L x 24 (54.28°, 62.31°, 63.41°)
- H-K-N x 24 (52.56°, 60.11°, 67.34°)
- J-J-Q x 12 (55.04°, 55.04°, 69.91°)
- M-M-O x 12 (58.80°, 58.80°, 62.40°)
- M-N-R x 24 (55.00°, 57.97°, 67.03°)
- P-P-Q x 12 (59.94°, 59.94°, 60.12°)
- P-R-S x 24 (57.85°, 58.95°, 63.19°)
- S-S-T x 12 (58.89°, 58.89°, 62.21°)
- T-T-T x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
8V Octahedron Dome Calculator
Geodesic 8V Octahedron Dome (Human is 170cm/5'7") |
L4 Octahedron Dome
|
|
|
- vertices/connectors: 145
- 4 x 3-way
- 29 x 4-way
- 112 x 6-way
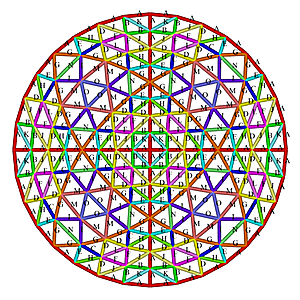
 L4 Octahedron Dome Construction Map
L4 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 64: 0.19603 (5.62°)
- B x 24: 0.19991 (5.74°)
- C x 24: 0.20044 (5.75°)
- D x 48: 0.21266 (6.10°)
- E x 24: 0.21671 (6.22°)
- F x 24: 0.21746 (6.24°)
- G x 48: 0.26105 (7.50°)
- H x 24: 0.26433 (7.59°)
- I x 24: 0.26899 (7.73°)
- J x 24: 0.27316 (7.85°)
- K x 12: 0.27590 (7.93°)
- L x 12: 0.27686 (7.96°)
- M x 24: 0.29180 (8.39°)
- N x 12: 0.29886 (8.59°)
- O x 12: 0.30151 (8.67°)
- total 400 struts (15 kinds)1)
- strut variance 53.8%
- faces: 256 (3-sided)
- A-A-K x 12 (45.27°, 45.27°, 89.47°)
- A-B-J x 24 (45.78°, 46.96°, 87.27°)
- A-D-H x 24 (47.00°, 52.53°, 80.47°)
- A-E-G x 24 (47.32°, 54.37°, 78.32°)
- B-B-K x 12 (46.36°, 46.36°, 87.28°)
- C-D-G x 24 (48.74°, 52.92°, 78.34°)
- C-E-H x 24 (48.00°, 53.47°, 78.53°)
- D-D-L x 12 (49.39°, 49.39°, 81.22°)
- D-F-J x 24 (49.80°, 51.36°, 78.84°)
- F-F-L x 12 (50.46°, 50.46°, 79.07°)
- G-G-N x 12 (55.08°, 55.08°, 69.83°)
- G-I-M x 24 (55.32°, 57.91°, 66.78°)
- I-I-N x 12 (56.25°, 56.25°, 67.50°)
- M-M-O x 12 (58.89°, 58.89°, 62.21°)
- O-O-O x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L4 Octahedron Dome Calculator
Geodesic L4 Octahedron Dome (Human is 170cm/5'7") |
Now the advantage of L3 vs 4V is more apparent, the L3 has various almost even horizontal bases where 4V has only one at 1/2 height.
So, let's explore 7/16 and 9/16 variants as well.
L4 7/16 Octahedron Dome
|
|
|
- vertices/connectors: 113
- 4 x 3-way
- 25 x 4-way
- 84 x 6-way
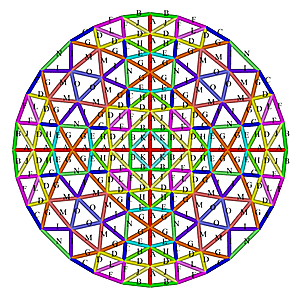
 L4 7/16 Octahedron Dome Construction Map
L4 7/16 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.19603 (5.62°)
- B x 16: 0.19991 (5.74°)
- C x 24: 0.20044 (5.75°)
- D x 40: 0.21266 (6.10°)
- E x 16: 0.21671 (6.22°)
- F x 24: 0.21746 (6.24°)
- G x 40: 0.26105 (7.50°)
- H x 16: 0.26433 (7.59°)
- I x 24: 0.26899 (7.73°)
- J x 16: 0.27316 (7.85°)
- K x 4: 0.27590 (7.93°)
- L x 12: 0.27686 (7.96°)
- M x 24: 0.29180 (8.39°)
- N x 12: 0.29886 (8.59°)
- O x 12: 0.30151 (8.67°)
- total 308 struts (15 kinds)1)
- strut variance 53.8%
- faces: 196 (3-sided)
- A-A-K x 4 (45.27°, 45.27°, 89.47°)
- A-B-J x 16 (45.78°, 46.96°, 87.27°)
- A-D-H x 16 (47.00°, 52.53°, 80.47°)
- A-E-G x 16 (47.32°, 54.37°, 78.32°)
- B-B-K x 4 (46.36°, 46.36°, 87.28°)
- C-D-G x 24 (48.74°, 52.92°, 78.34°)
- C-E-H x 16 (48.00°, 53.47°, 78.53°)
- D-D-L x 12 (49.39°, 49.39°, 81.22°)
- D-F-J x 16 (49.80°, 51.36°, 78.84°)
- F-F-L x 12 (50.46°, 50.46°, 79.07°)
- G-G-N x 8 (55.08°, 55.08°, 69.83°)
- G-I-M x 24 (55.32°, 57.91°, 66.78°)
- I-I-N x 12 (56.25°, 56.25°, 67.50°)
- M-M-O x 12 (58.89°, 58.89°, 62.21°)
- O-O-O x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.805 or 40.25% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L4 7/16 Octahedron Dome Calculator
Geodesic L4 7/16 Octahedron Dome (Human is 170cm/5'7") |
L4 9/16 Octahedron Dome
|
|
|
- vertices/connectors: 173
- 29 x 4-way
- 4 x 5-way
- 140 x 6-way
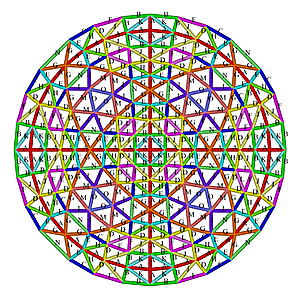
 L4 9/16 Octahedron Dome Construction Map
L4 9/16 Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 68: 0.19603 (5.62°)
- B x 40: 0.19991 (5.74°)
- C x 32: 0.20044 (5.75°)
- D x 56: 0.21266 (6.10°)
- E x 32: 0.21671 (6.22°)
- F x 32: 0.21746 (6.24°)
- G x 56: 0.26105 (7.50°)
- H x 32: 0.26433 (7.59°)
- I x 24: 0.26899 (7.73°)
- J x 32: 0.27316 (7.85°)
- K x 20: 0.27590 (7.93°)
- L x 12: 0.27686 (7.96°)
- M x 24: 0.29180 (8.39°)
- N x 16: 0.29886 (8.59°)
- O x 12: 0.30151 (8.67°)
- total 488 struts (15 kinds)1)
- strut variance 53.8%
- faces: 316 (3-sided)
- A-A-K x 20 (45.27°, 45.27°, 89.47°)
- A-B-J x 32 (45.78°, 46.96°, 87.27°)
- A-D-H x 32 (47.00°, 52.53°, 80.47°)
- A-E-G x 32 (47.32°, 54.37°, 78.32°)
- B-B-K x 20 (46.36°, 46.36°, 87.28°)
- C-D-G x 24 (48.74°, 52.92°, 78.34°)
- C-E-H x 32 (48.00°, 53.47°, 78.53°)
- D-D-L x 12 (49.39°, 49.39°, 81.22°)
- D-F-J x 32 (49.80°, 51.36°, 78.84°)
- F-F-L x 12 (50.46°, 50.46°, 79.07°)
- G-G-N x 16 (55.08°, 55.08°, 69.83°)
- G-I-M x 24 (55.32°, 57.91°, 66.78°)
- I-I-N x 12 (56.25°, 56.25°, 67.50°)
- M-M-O x 12 (58.89°, 58.89°, 62.21°)
- O-O-O x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.211 or 60.57% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L4 9/16 Octahedron Dome Calculator
Geodesic L4 9/16 Octahedron Dome (Human is 170cm/5'7") |
The L4 6/16 and 10/16 Octahedron Dome would be also possible, but the leveling gets already bigger as you see.
|
|
9V Octahedron Dome
|
|
|
- vertices/connectors: 181
- 4 x 3-way
- 33 x 4-way
- 144 x 6-way

 9V Octahedron Dome Construction Map
9V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.12427 (3.56°)
- B x 24: 0.14146 (4.06°)
- C x 16: 0.15379 (4.41°)
- D x 24: 0.16250 (4.66°)
- E x 12: 0.17541 (5.03°)
- F x 24: 0.17837 (5.12°)
- G x 16: 0.18508 (5.31°)
- H x 24: 0.18597 (5.34°)
- I x 24: 0.19519 (5.60°)
- J x 48: 0.20635 (5.92°)
- K x 40: 0.21070 (6.05°)
- L x 48: 0.21572 (6.19°)
- M x 20: 0.22086 (6.34°)
- N x 24: 0.23223 (6.67°)
- O x 48: 0.24080 (6.92°)
- P x 48: 0.24592 (7.06°)
- Q x 24: 0.26261 (7.55°)
- R x 24: 0.26495 (7.61°)
- total 504 struts (18 kinds)1)
- strut variance 113.2%
- faces: 324 (3-sided)
- A-A-E x 12 (45.13°, 45.13°, 89.75°)
- B-B-E x 12 (51.70°, 51.70°, 76.60°)
- B-C-I x 24 (45.97°, 51.39°, 82.64°)
- D-F-I x 24 (51.32°, 58.99°, 69.68°)
- D-G-K x 24 (47.94°, 57.75°, 74.30°)
- F-F-M x 12 (51.75°, 51.75°, 76.50°)
- H-K-L x 48 (51.71°, 62.76°, 65.53°)
- J-J-M x 24 (57.65°, 57.65°, 64.70°)
- J-L-O x 48 (53.42°, 57.05°, 69.53°)
- N-O-P x 48 (56.98°, 60.40°, 62.62°)
- P-P-Q x 24 (57.73°, 57.73°, 64.55°)
- Q-R-R x 24 (59.40°, 60.30°, 60.30°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
9V Octahedron Dome Calculator
Geodesic 9V Octahedron Dome (Human is 170cm/5'7") |
3V.3V Octahedron Dome
|
|
|
- vertices/connectors: 181
- 4 x 3-way
- 33 x 4-way
- 144 x 6-way
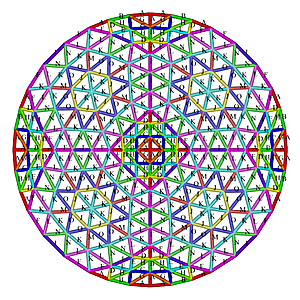
 3V.3V Octahedron Dome Construction Map
3V.3V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.15315 (4.39°)
- B x 16: 0.15689 (4.50°)
- C x 24: 0.15697 (4.50°)
- D x 24: 0.15706 (4.50°)
- E x 24: 0.16057 (4.60°)
- F x 40: 0.21070 (6.05°)
- G x 12: 0.21595 (6.20°)
- H x 24: 0.21723 (6.24°)
- I x 20: 0.22086 (6.34°)
- J x 24: 0.22224 (6.38°)
- K x 96: 0.22365 (6.42°)
- L x 48: 0.23512 (6.75°)
- M x 24: 0.23594 (6.77°)
- N x 48: 0.23610 (6.78°)
- O x 48: 0.23760 (6.82°)
- total 504 struts (15 kinds)1)
- strut variance 55.1%
- faces: 324 (3-sided)
- A-A-G x 12 (45.17°, 45.17°, 89.65°)
- A-D-F x 24 (46.46°, 48.02°, 85.52°)
- B-C-H x 24 (46.20°, 46.24°, 87.57°)
- C-C-G x 12 (46.54°, 46.54°, 86.93°)
- D-E-H x 24 (46.20°, 47.55°, 86.25°)
- E-E-I x 12 (46.55°, 46.55°, 86.90°)
- F-K-L x 48 (54.62°, 59.91°, 65.47°)
- I-N-N x 24 (55.78°, 62.11°, 62.11°)
- J-K-K x 24 (59.59°, 60.21°, 60.21°)
- J-O-O x 24 (55.76°, 62.12°, 62.12°)
- K-L-N x 48 (56.66°, 61.45°, 61.90°)
- K-M-O x 48 (56.36°, 61.44°, 62.21°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V.3V Octahedron Dome Calculator
Geodesic 3V.3V Octahedron Dome (Human is 170cm/5'7") |
10V Octahedron Dome
|
|
|
- vertices/connectors: 221
- 4 x 3-way
- 37 x 4-way
- 180 x 6-way
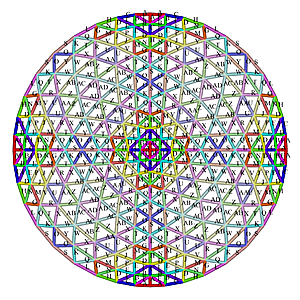
 10V Octahedron Dome Construction Map
10V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.11060 (3.17°)
- B x 24: 0.12408 (3.56°)
- C x 16: 0.13422 (3.85°)
- D x 24: 0.14037 (4.02°)
- E x 24: 0.15305 (4.39°)
- F x 12: 0.15617 (4.48°)
- G x 24: 0.15897 (4.56°)
- H x 16: 0.15974 (4.58°)
- I x 24: 0.17214 (4.94°)
- J x 24: 0.17475 (5.01°)
- K x 24: 0.17715 (5.08°)
- L x 16: 0.18286 (5.25°)
- M x 24: 0.18357 (5.27°)
- N x 24: 0.18563 (5.33°)
- O x 24: 0.18984 (5.45°)
- P x 12: 0.19245 (5.52°)
- Q x 24: 0.19270 (5.53°)
- R x 24: 0.19673 (5.65°)
- S x 16: 0.19708 (5.66°)
- T x 24: 0.20840 (5.98°)
- U x 24: 0.20865 (5.99°)
- V x 24: 0.20967 (6.02°)
- W x 24: 0.21329 (6.12°)
- X x 24: 0.21808 (6.26°)
- Y x 12: 0.21822 (6.26°)
- Z x 24: 0.22923 (6.58°)
- AA x 12: 0.22942 (6.59°)
- AB x 24: 0.23096 (6.63°)
- AC x 24: 0.23738 (6.82°)
- AD x 12: 0.24254 (6.97°)
- total 620 struts (30 kinds)1)
- strut variance 119.3%
- faces: 400 (3-sided)
- A-A-F x 12 (45.08°, 45.08°, 89.84°)
- AA-U-U x 12 (66.68°, 56.66°, 56.66°)
- AA-Z-Z x 12 (60.06°, 59.97°, 59.97°)
- AB-AC-Z x 24 (59.32°, 62.11°, 58.57°)
- AB-W-X x 24 (64.74°, 56.62°, 58.64°)
- AC-AC-AD x 12 (59.29°, 59.29°, 61.43°)
- AD-AD-AD x 4 (60.00°, 60.00°, 60.00°)
- B-B-F x 12 (51.00°, 51.00°, 78.00°)
- B-C-I x 24 (45.76°, 50.78°, 83.46°)
- D-E-I x 24 (50.76°, 57.56°, 71.68°)
- D-H-N x 24 (47.25°, 56.64°, 76.11°)
- E-E-P x 12 (51.02°, 51.02°, 77.97°)
- G-L-Q x 24 (50.01°, 61.80°, 68.20°)
- G-M-N x 24 (51.02°, 63.84°, 65.14°)
- J-J-P x 12 (56.57°, 56.57°, 66.86°)
- J-M-V x 24 (52.23°, 56.18°, 71.59°)
- K-O-S x 24 (54.48°, 60.66°, 64.86°)
- K-Q-T x 24 (52.26°, 59.31°, 68.43°)
- O-O-Y x 12 (54.91°, 54.91°, 70.17°)
- R-T-X x 24 (54.87°, 60.06°, 65.07°)
- R-U-V x 24 (56.08°, 61.70°, 62.22°)
- W-W-Y x 12 (59.24°, 59.24°, 61.53°)
- 22 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
10V Octahedron Dome Calculator
Geodesic 10V Octahedron Dome (Human is 170cm/5'7") |
2V.5V Octahedron Dome
|
|
|
- vertices/connectors: 221
- 4 x 3-way
- 37 x 4-way
- 180 x 6-way
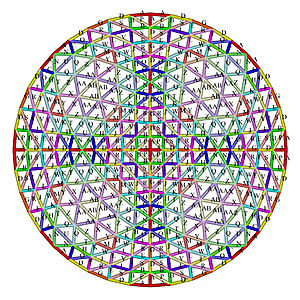
 2V.5V Octahedron Dome Construction Map
2V.5V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.14897 (4.27°)
- B x 24: 0.15701 (4.50°)
- C x 24: 0.15942 (4.57°)
- D x 32: 0.16077 (4.61°)
- E x 24: 0.16200 (4.65°)
- F x 24: 0.16287 (4.67°)
- G x 16: 0.16512 (4.74°)
- H x 24: 0.16655 (4.78°)
- I x 24: 0.16939 (4.86°)
- J x 24: 0.17295 (4.96°)
- K x 24: 0.17327 (4.97°)
- L x 24: 0.17393 (4.99°)
- M x 24: 0.17615 (5.05°)
- N x 24: 0.18984 (5.45°)
- O x 24: 0.20577 (5.91°)
- P x 12: 0.21009 (6.03°)
- Q x 24: 0.21329 (6.12°)
- R x 24: 0.21561 (6.19°)
- S x 24: 0.21702 (6.23°)
- T x 24: 0.21808 (6.26°)
- U x 12: 0.21822 (6.26°)
- V x 12: 0.22654 (6.50°)
- W x 24: 0.22702 (6.52°)
- X x 24: 0.22923 (6.58°)
- Y x 12: 0.22942 (6.59°)
- Z x 24: 0.23096 (6.63°)
- AA x 24: 0.23738 (6.82°)
- AB x 12: 0.24254 (6.97°)
- total 620 struts (28 kinds)1)
- strut variance 62.8%
- faces: 400 (3-sided)
- A-A-P x 12 (45.17°, 45.17°, 89.66°)
- A-C-N x 24 (49.58°, 54.54°, 75.88°)
- AA-AA-AB x 12 (59.29°, 59.29°, 61.43°)
- AA-X-Z x 24 (62.11°, 58.57°, 59.32°)
- AB-AB-AB x 4 (60.00°, 60.00°, 60.00°)
- B-B-P x 12 (48.00°, 48.00°, 84.00°)
- B-D-S x 24 (46.21°, 47.67°, 86.12°)
- C-H-O x 24 (49.32°, 52.43°, 78.26°)
- D-F-O x 24 (50.07°, 50.98°, 78.95°)
- E-G-R x 24 (48.15°, 49.39°, 82.46°)
- E-I-S x 24 (47.63°, 50.59°, 81.78°)
- F-J-R x 24 (48.05°, 52.12°, 79.83°)
- H-K-T x 24 (48.75°, 51.45°, 79.80°)
- I-I-V x 12 (48.05°, 48.05°, 83.91°)
- J-L-W x 24 (48.92°, 49.31°, 81.77°)
- K-M-W x 24 (48.94°, 50.06°, 81.00°)
- L-L-V x 12 (49.37°, 49.37°, 81.27°)
- M-M-Y x 12 (49.39°, 49.39°, 81.23°)
- N-N-U x 12 (54.91°, 54.91°, 70.17°)
- Q-Q-U x 12 (59.24°, 59.24°, 61.53°)
- Q-T-Z x 24 (56.62°, 58.64°, 64.74°)
- X-X-Y x 12 (59.97°, 59.97°, 60.06°)
- 22 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V.5V Octahedron Dome Calculator
Geodesic 2V.5V Octahedron Dome (Human is 170cm/5'7") |
2V.5V Octahedron Dome
|
|
|
- vertices/connectors: 221
- 4 x 3-way
- 37 x 4-way
- 180 x 6-way
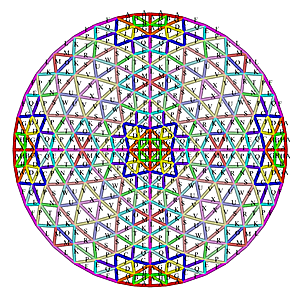
 5V.2V Octahedron Dome Construction Map
5V.2V Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.12241 (3.51°)
- B x 24: 0.12334 (3.54°)
- C x 48: 0.15757 (4.52°)
- D x 24: 0.15923 (4.57°)
- E x 24: 0.15977 (4.58°)
- F x 32: 0.17130 (4.91°)
- G x 24: 0.17214 (4.94°)
- H x 12: 0.17279 (4.96°)
- I x 24: 0.17332 (4.97°)
- J x 12: 0.17365 (4.98°)
- K x 48: 0.19523 (5.60°)
- L x 16: 0.19708 (5.66°)
- M x 24: 0.19810 (5.68°)
- N x 24: 0.19866 (5.70°)
- O x 12: 0.19993 (5.74°)
- P x 48: 0.20119 (5.77°)
- Q x 24: 0.20290 (5.82°)
- R x 24: 0.20452 (5.87°)
- S x 48: 0.21981 (6.31°)
- T x 24: 0.22285 (6.40°)
- U x 24: 0.22431 (6.44°)
- V x 24: 0.23738 (6.82°)
- W x 12: 0.24154 (6.94°)
- X x 12: 0.24254 (6.97°)
- total 620 struts (24 kinds)1)
- strut variance 98.1%
- faces: 400 (3-sided)
- A-A-H x 12 (45.10°, 45.10°, 89.80°)
- A-B-G x 24 (45.32°, 45.75°, 88.93°)
- B-B-H x 12 (45.51°, 45.51°, 88.97°)
- C-C-J x 12 (56.58°, 56.58°, 66.84°)
- C-D-G x 24 (56.65°, 57.54°, 65.81°)
- C-F-Q x 24 (48.92°, 55.02°, 76.05°)
- C-I-P x 24 (49.08°, 56.19°, 74.73°)
- D-D-J x 12 (56.96°, 56.96°, 66.08°)
- E-F-P x 24 (50.02°, 55.23°, 74.75°)
- E-I-Q x 24 (49.51°, 55.56°, 74.93°)
- K-K-O x 12 (59.20°, 59.20°, 61.60°)
- K-L-M x 24 (59.20°, 60.15°, 60.66°)
- K-P-T x 24 (54.53°, 57.09°, 68.38°)
- K-R-S x 24 (54.64°, 58.69°, 66.67°)
- M-M-O x 12 (59.70°, 59.70°, 60.60°)
- N-P-S x 24 (56.12°, 57.20°, 66.68°)
- N-R-T x 24 (55.22°, 57.71°, 67.07°)
- S-S-W x 12 (56.68°, 56.68°, 66.65°)
- S-U-V x 24 (56.77°, 58.61°, 64.62°)
- U-U-W x 12 (57.43°, 57.43°, 65.14°)
- V-V-X x 12 (59.29°, 59.29°, 61.43°)
- X-X-X x 4 (60.00°, 60.00°, 60.00°)
- 22 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V.2V Octahedron Dome Calculator
Geodesic 5V.2V Octahedron Dome (Human is 170cm/5'7") |
The Cube
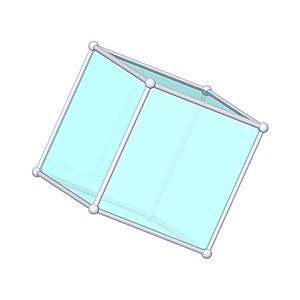  Cube |
- Uniform Polyhedron: U6
- aka Hexahedron
- Platonic Solid
- Platonic Element: Earth
- Vertices: 8
- Edges: 12
- Faces: 6
- Wythoff symbol: 3|2 4
- Symmetry Group: octahedral
- Vertex Configuration: {4, 4, 4}
- Dual: octahedron
- V: s3
- A: s2 * 6
- rinner: s / 2
- router: s / 2 * √3

Preparing the Cube
1V/L1 Cube Dome
|
|
|
- vertices/connectors: 10
- 2 x 3-way
- 6 x 4-way
- 2 x 6-way
 1V Cube Dome Construction Map
1V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 14: 0.91940 (27.37°)
- B x 7: 1.15470 (35.26°)
- total 21 struts (2 kinds)1)
- strut variance 25.6%
- faces: 12 (3-sided)
- A-A-B x 12 (51.10°, 51.10°, 77.80°)
- diameter: 2.000, radius: 1.000
- height: 0.817 or 40.83% of diameter
1V Cube Dome Calculator
Geodesic 1V Cube Dome (Human is 170cm/5'7") |
2V/L2 Cube Dome
|
|
|
- vertices/connectors: 31
- 2 x 3-way
- 12 x 4-way
- 17 x 6-way
 2V Cube Dome Construction Map
2V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.47313 (13.68°)
- B x 24: 0.53327 (15.46°)
- C x 14: 0.60581 (17.63°)
- D x 12: 0.65012 (18.97°)
- total 78 struts (4 kinds)1)
- strut variance 37.4%
- faces: 48 (3-sided)
- A-A-D x 12 (46.60°, 46.60°, 86.80°)
- A-B-C x 24 (48.57°, 57.69°, 73.75°)
- B-B-D x 12 (52.45°, 52.45°, 75.11°)
- 3 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V Cube Dome Calculator
Geodesic 2V Cube Dome (Human is 170cm/5'7") |
3V Cube Dome
|
|
|
- vertices/connectors: 64
- 2 x 3-way
- 18 x 4-way
- 44 x 6-way
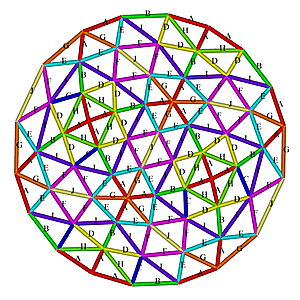
 3V Cube Dome Construction Map
3V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.30559 (8.79°)
- B x 14: 0.34007 (9.79°)
- C x 6: 0.34314 (9.88°)
- D x 18: 0.34315 (9.88°)
- E x 24: 0.34511 (9.94°)
- F x 24: 0.36954 (10.65°)
- G x 14: 0.38165 (11.00°)
- H x 12: 0.42710 (12.33°)
- I x 24: 0.43771 (12.64°)
- J x 7: 0.45883 (13.26°)
- total 171 struts (10 kinds)1)
- strut variance 50.1%
- faces: 108 (3-sided)
- A-A-H x 12 (45.67°, 45.67°, 88.66°)
- A-E-G x 24 (49.42°, 59.06°, 71.52°)
- B-C-I x 6 (49.86°, 50.46°, 79.68°)
- B-D-I x 18 (49.85°, 50.48°, 79.67°)
- C-D-H x 6 (51.50°, 51.52°, 76.97°)
- D-D-H x 6 (51.52°, 51.52°, 76.96°)
- E-F-I x 24 (49.74°, 54.80°, 75.46°)
- F-F-J x 12 (51.62°, 51.62°, 76.75°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.973 or 48.67% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V Cube Dome Calculator
Geodesic 3V Cube Dome (Human is 170cm/5'7") |
4V Cube Dome
|
|
|
- vertices/connectors: 109
- 2 x 3-way
- 24 x 4-way
- 83 x 6-way
 4V Cube Dome Construction Map
4V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.22393 (6.43°)
- B x 24: 0.24654 (7.08°)
- C x 24: 0.25137 (7.22°)
- D x 28: 0.25259 (7.26°)
- E x 24: 0.25756 (7.40°)
- F x 24: 0.26734 (7.68°)
- G x 14: 0.27477 (7.90°)
- H x 24: 0.27584 (7.93°)
- I x 24: 0.28059 (8.06°)
- J x 24: 0.31367 (9.02°)
- K x 12: 0.31469 (9.05°)
- L x 24: 0.32956 (9.48°)
- M x 14: 0.33820 (9.74°)
- N x 12: 0.35141 (10.12°)
- total 300 struts (14 kinds)1)
- strut variance 56.9%
- faces: 192 (3-sided)
- A-A-K x 12 (45.35°, 45.35°, 89.30°)
- A-C-G x 24 (50.12°, 59.51°, 70.37°)
- B-B-K x 12 (50.33°, 50.33°, 79.34°)
- B-D-L x 24 (47.88°, 49.47°, 82.65°)
- C-F-J x 24 (50.51°, 55.14°, 74.36°)
- D-E-J x 24 (51.34°, 52.78°, 75.88°)
- E-H-L x 24 (49.39°, 54.37°, 76.24°)
- F-I-M x 24 (50.13°, 53.68°, 76.19°)
- H-H-N x 12 (50.43°, 50.43°, 79.15°)
- I-I-N x 12 (51.23°, 51.23°, 77.53°)
- 10 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
4V Cube Dome Calculator
Geodesic 4V Cube Dome (Human is 170cm/5'7") |
L3 Cube Dome
|
|
|
- vertices/connectors: 109
- 2 x 3-way
- 24 x 4-way
- 83 x 6-way
 L3 Cube Dome Construction Map
L3 Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 56: 0.23826 (6.84°)
- B x 24: 0.24530 (7.05°)
- C x 24: 0.24658 (7.08°)
- D x 48: 0.26908 (7.73°)
- E x 24: 0.27641 (7.94°)
- F x 24: 0.27864 (8.01°)
- G x 28: 0.30653 (8.82°)
- H x 24: 0.31291 (9.00°)
- I x 24: 0.32956 (9.48°)
- J x 12: 0.33455 (9.63°)
- K x 12: 0.33727 (9.71°)
- total 300 struts (11 kinds)1)
- strut variance 41.5%
- faces: 192 (3-sided)
- A-A-J x 12 (45.41°, 45.41°, 89.18°)
- A-B-I x 24 (46.15°, 47.93°, 85.92°)
- A-D-H x 24 (47.61°, 56.51°, 75.88°)
- A-E-G x 24 (47.92°, 59.41°, 72.67°)
- B-B-J x 12 (47.00°, 47.00°, 86.00°)
- C-D-G x 24 (50.22°, 57.00°, 72.78°)
- C-E-H x 24 (48.99°, 57.76°, 73.24°)
- D-D-K x 12 (51.19°, 51.19°, 77.62°)
- D-F-I x 24 (51.69°, 54.33°, 73.97°)
- F-F-K x 12 (52.75°, 52.75°, 74.51°)
- 10 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 Cube Dome Calculator
Geodesic L3 Cube Dome (Human is 170cm/5'7") |
5V Cube Dome
|
|
|
- vertices/connectors: 166
- 2 x 3-way
- 30 x 4-way
- 134 x 6-way

 5V Cube Dome Construction Map
5V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.17629 (5.06°)
- B x 24: 0.19100 (5.48°)
- C x 24: 0.19686 (5.65°)
- D x 28: 0.19765 (5.67°)
- E x 24: 0.20103 (5.77°)
- F x 24: 0.20327 (5.83°)
- G x 38: 0.20588 (5.91°)
- H x 14: 0.21382 (6.14°)
- I x 24: 0.21400 (6.14°)
- J x 24: 0.21992 (6.31°)
- K x 24: 0.22028 (6.32°)
- L x 24: 0.22264 (6.39°)
- M x 24: 0.22437 (6.44°)
- N x 24: 0.24051 (6.91°)
- O x 12: 0.24834 (7.13°)
- P x 24: 0.25832 (7.42°)
- Q x 14: 0.26002 (7.47°)
- R x 24: 0.26089 (7.50°)
- S x 24: 0.27779 (7.98°)
- T x 12: 0.27793 (7.99°)
- U x 7: 0.28006 (8.05°)
- total 465 struts (21 kinds)1)
- strut variance 58.9%
- faces: 300 (3-sided)
- A-A-O x 12 (45.24°, 45.24°, 89.53°)
- A-C-H x 24 (50.64°, 59.71°, 69.65°)
- B-B-O x 12 (49.46°, 49.46°, 81.08°)
- B-D-R x 24 (46.76°, 48.91°, 84.33°)
- C-G-N x 24 (51.64°, 55.08°, 73.28°)
- D-F-N x 24 (52.06°, 54.23°, 73.71°)
- E-G-P x 24 (49.76°, 51.44°, 78.80°)
- E-I-R x 24 (48.86°, 53.30°, 77.84°)
- F-J-P x 24 (49.52°, 55.36°, 75.12°)
- G-K-Q x 24 (49.93°, 54.97°, 75.10°)
- I-I-T x 12 (49.51°, 49.51°, 80.98°)
- J-L-S x 24 (50.68°, 51.55°, 77.77°)
- K-M-S x 24 (50.68°, 52.00°, 77.31°)
- L-L-T x 12 (51.38°, 51.38°, 77.25°)
- M-M-U x 12 (51.38°, 51.38°, 77.23°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.990 or 49.51% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V Cube Dome Calculator
Geodesic 5V Cube Dome (Human is 170cm/5'7") |
6V Cube Dome
|
|
|
- vertices/connectors: 235
- 2 x 3-way
- 36 x 4-way
- 197 x 6-way

 6V Cube Dome Construction Map
6V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.14523 (4.16°)
- B x 24: 0.15547 (4.46°)
- C x 28: 0.16126 (4.62°)
- D x 24: 0.16153 (4.63°)
- E x 24: 0.16348 (4.69°)
- F x 24: 0.16630 (4.77°)
- G x 24: 0.16695 (4.79°)
- H x 24: 0.16766 (4.81°)
- I x 28: 0.17066 (4.90°)
- J x 24: 0.17291 (4.96°)
- K x 14: 0.17475 (5.01°)
- L x 48: 0.17945 (5.15°)
- M x 24: 0.18094 (5.19°)
- N x 24: 0.18189 (5.22°)
- O x 24: 0.18285 (5.25°)
- P x 24: 0.18335 (5.26°)
- Q x 24: 0.18806 (5.40°)
- R x 24: 0.18829 (5.40°)
- S x 24: 0.19379 (5.56°)
- T x 12: 0.20485 (5.88°)
- U x 14: 0.20865 (5.99°)
- V x 24: 0.20898 (6.00°)
- W x 24: 0.21479 (6.17°)
- X x 24: 0.21657 (6.22°)
- Y x 24: 0.22440 (6.44°)
- Z x 12: 0.22766 (6.54°)
- AA x 14: 0.23096 (6.63°)
- AB x 24: 0.23140 (6.64°)
- AC x 12: 0.23682 (6.80°)
- total 666 struts (29 kinds)1)
- strut variance 63.1%
- faces: 432 (3-sided)
- A-A-T x 12 (45.12°, 45.12°, 89.75°)
- A-D-K x 24 (50.99°, 59.80°, 69.21°)
- AA-O-Q x 24 (77.00°, 50.49°, 52.51°)
- AB-M-N x 24 (79.26°, 50.18°, 50.56°)
- AB-P-R x 24 (76.99°, 50.55°, 52.45°)
- AC-Q-Q x 12 (78.02°, 50.99°, 50.99°)
- AC-R-R x 12 (77.92°, 51.04°, 51.04°)
- B-B-T x 12 (48.79°, 48.79°, 82.42°)
- B-C-W x 24 (46.18°, 48.46°, 85.36°)
- C-G-S x 24 (52.48°, 55.16°, 72.36°)
- D-F-S x 24 (52.62°, 54.91°, 72.47°)
- E-I-X x 24 (48.17°, 51.07°, 80.77°)
- E-J-W x 24 (48.41°, 52.28°, 79.31°)
- F-L-U x 24 (50.05°, 55.79°, 74.16°)
- G-L-V x 24 (50.19°, 55.66°, 74.15°)
- H-I-V x 24 (51.21°, 52.51°, 76.28°)
- H-N-X x 24 (48.82°, 54.73°, 76.45°)
- J-J-Z x 12 (48.82°, 48.82°, 82.37°)
- L-O-Y x 24 (51.03°, 52.43°, 76.53°)
- L-P-Y x 24 (50.99°, 52.60°, 76.41°)
- M-M-Z x 12 (51.00°, 51.00°, 78.00°)
- 21 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
6V Cube Dome Calculator
Geodesic 6V Cube Dome (Human is 170cm/5'7") |
2V.3V Cube Dome
|
|
|
- vertices/connectors: 235
- 2 x 3-way
- 36 x 4-way
- 197 x 6-way

 2V.3V Cube Dome Construction Map
2V.3V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 56: 0.15768 (4.52°)
- B x 28: 0.16179 (4.64°)
- C x 24: 0.16188 (4.64°)
- D x 24: 0.16198 (4.65°)
- E x 24: 0.16341 (4.69°)
- F x 24: 0.16345 (4.69°)
- G x 24: 0.16505 (4.73°)
- H x 24: 0.16580 (4.76°)
- I x 48: 0.17771 (5.10°)
- J x 24: 0.18291 (5.25°)
- K x 24: 0.18312 (5.25°)
- L x 24: 0.18365 (5.27°)
- M x 24: 0.18424 (5.29°)
- N x 24: 0.18444 (5.29°)
- O x 24: 0.18608 (5.34°)
- P x 24: 0.18737 (5.38°)
- Q x 28: 0.20184 (5.79°)
- R x 24: 0.20777 (5.96°)
- S x 24: 0.20826 (5.98°)
- T x 24: 0.20976 (6.02°)
- U x 14: 0.21071 (6.05°)
- V x 24: 0.21657 (6.22°)
- W x 12: 0.22230 (6.38°)
- X x 24: 0.22371 (6.42°)
- Y x 12: 0.22389 (6.43°)
- Z x 24: 0.22533 (6.47°)
- AA x 12: 0.22766 (6.54°)
- total 666 struts (27 kinds)1)
- strut variance 44.4%
- faces: 432 (3-sided)
- A-A-W x 12 (45.19°, 45.19°, 89.63°)
- A-D-V x 24 (46.52°, 48.19°, 85.29°)
- A-I-R x 24 (47.51°, 56.19°, 76.31°)
- A-K-Q x 24 (48.07°, 59.75°, 72.18°)
- AA-H-H x 12 (86.73°, 46.63°, 46.63°)
- AA-P-P x 12 (74.82°, 52.59°, 52.59°)
- B-C-X x 24 (46.27°, 46.30°, 87.43°)
- B-J-S x 24 (48.33°, 57.60°, 74.07°)
- C-C-W x 12 (46.64°, 46.64°, 86.71°)
- D-H-X x 24 (46.26°, 47.68°, 86.06°)
- E-J-R x 24 (48.94°, 57.56°, 73.51°)
- E-L-T x 24 (48.51°, 57.37°, 74.12°)
- F-I-Q x 24 (50.55°, 57.06°, 72.38°)
- F-O-T x 24 (48.33°, 58.24°, 73.44°)
- G-K-S x 24 (49.38°, 57.34°, 73.28°)
- G-O-U x 24 (48.69°, 57.85°, 73.46°)
- I-I-Y x 12 (50.95°, 50.95°, 78.10°)
- I-N-V x 24 (51.85°, 54.69°, 73.45°)
- L-M-Z x 24 (52.14°, 52.34°, 75.53°)
- M-M-Y x 12 (52.57°, 52.57°, 74.86°)
- N-P-Z x 24 (52.10°, 53.31°, 74.59°)
- 21 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V.3V Cube Dome Calculator
Geodesic 2V.3V Cube Dome (Human is 170cm/5'7") |
3V.2V Cube Dome
|
|
|
- vertices/connectors: 235
- 2 x 3-way
- 36 x 4-way
- 197 x 6-way

 3V.2V Cube Dome Construction Map
3V.2V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 56: 0.15325 (4.39°)
- B x 24: 0.15508 (4.45°)
- C x 24: 0.15535 (4.45°)
- D x 28: 0.17066 (4.90°)
- E x 48: 0.17221 (4.94°)
- F x 72: 0.17320 (4.97°)
- G x 48: 0.17469 (5.01°)
- H x 24: 0.17506 (5.02°)
- I x 24: 0.17606 (5.05°)
- J x 48: 0.18557 (5.32°)
- K x 24: 0.18823 (5.40°)
- L x 24: 0.18867 (5.41°)
- M x 28: 0.19171 (5.50°)
- N x 24: 0.19338 (5.55°)
- O x 24: 0.21479 (6.17°)
- P x 12: 0.21609 (6.20°)
- Q x 12: 0.21676 (6.22°)
- R x 48: 0.22019 (6.32°)
- S x 24: 0.22212 (6.38°)
- T x 24: 0.22243 (6.39°)
- U x 14: 0.23096 (6.63°)
- V x 12: 0.23343 (6.70°)
- total 666 struts (22 kinds)1)
- strut variance 52.3%
- faces: 432 (3-sided)
- A-A-P x 12 (45.15°, 45.15°, 89.71°)
- A-B-O x 24 (45.47°, 46.20°, 88.33°)
- A-F-N x 24 (49.02°, 58.60°, 72.38°)
- A-H-M x 24 (49.12°, 59.79°, 71.10°)
- B-B-P x 12 (45.84°, 45.84°, 88.32°)
- C-F-M x 24 (50.06°, 58.77°, 71.17°)
- C-H-N x 24 (49.55°, 59.09°, 71.37°)
- D-E-S x 24 (49.34°, 49.93°, 80.74°)
- D-G-R x 24 (49.60°, 51.20°, 79.21°)
- E-E-Q x 12 (50.99°, 50.99°, 78.03°)
- E-F-R x 24 (50.19°, 50.59°, 79.21°)
- E-G-O x 24 (51.22°, 52.27°, 76.51°)
- F-G-S x 24 (50.03°, 50.63°, 79.34°)
- F-J-T x 24 (49.23°, 54.25°, 76.52°)
- F-K-R x 24 (49.43°, 55.62°, 74.95°)
- G-G-Q x 12 (51.65°, 51.65°, 76.70°)
- I-J-R x 24 (50.56°, 54.49°, 74.95°)
- I-K-T x 24 (49.95°, 54.89°, 75.17°)
- J-J-V x 12 (51.04°, 51.04°, 77.92°)
- J-L-U x 24 (51.29°, 52.50°, 76.21°)
- L-L-V x 12 (51.80°, 51.80°, 76.40°)
- 21 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V.2V Cube Dome Calculator
Geodesic 3V.2V Cube Dome (Human is 170cm/5'7") |
7V Cube Dome
|
|
|
- vertices/connectors: 316
- 2 x 3-way
- 42 x 4-way
- 272 x 6-way

 7V Cube Dome Construction Map
7V Cube Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 28: 0.12343 (3.54°)
- B x 24: 0.13093 (3.75°)
- C x 28: 0.13574 (3.89°)
- D x 24: 0.13685 (3.92°)
- E x 24: 0.13724 (3.93°)
- F x 24: 0.13907 (3.99°)
- G x 24: 0.14129 (4.05°)
- H x 24: 0.14148 (4.06°)
- I x 24: 0.14293 (4.10°)
- J x 24: 0.14432 (4.14°)
- K x 28: 0.14437 (4.14°)
- L x 14: 0.14749 (4.23°)
- M x 14: 0.14764 (4.23°)
- N x 24: 0.15012 (4.30°)
- O x 24: 0.15069 (4.32°)
- P x 24: 0.15101 (4.33°)
- Q x 24: 0.15272 (4.38°)
- R x 24: 0.15313 (4.39°)
- S x 24: 0.15455 (4.43°)
- T x 24: 0.15467 (4.44°)
- U x 24: 0.15525 (4.45°)
- V x 24: 0.15929 (4.57°)
- W x 24: 0.15968 (4.58°)
- X x 24: 0.15992 (4.59°)
- Y x 24: 0.16053 (4.60°)
- Z x 24: 0.16165 (4.64°)
- AA x 24: 0.16180 (4.64°)
- AB x 14: 0.17323 (4.97°)
- AC x 24: 0.17410 (4.99°)
- AD x 12: 0.17422 (5.00°)
- AE x 24: 0.18209 (5.22°)
- AF x 24: 0.18242 (5.23°)
- AG x 24: 0.18518 (5.31°)
- AH x 24: 0.18614 (5.34°)
- AI x 8: 0.19194 (5.51°)
- AJ x 4: 0.19195 (5.51°)
- AK x 14: 0.19327 (5.55°)
- AL x 24: 0.19451 (5.58°)
- AM x 24: 0.19653 (5.64°)
- AN x 7: 0.20101 (5.77°)
- AO x 24: 0.20124 (5.77°)
- AP x 12: 0.20240 (5.81°)
- total 903 struts (42 kinds)1)
- strut variance 64.0%
- faces: 588 (3-sided)
- A-A-AD x 12 (45.10°, 45.10°, 89.79°)
- A-D-M x 24 (51.26°, 59.85°, 68.90°)
- AA-C-G x 24 (71.45°, 52.67°, 55.89°)
- AA-D-F x 24 (71.80°, 53.44°, 54.76°)
- AB-F-O x 24 (73.28°, 50.28°, 56.44°)
- AC-G-N x 24 (73.31°, 51.02°, 55.67°)
- AC-I-K x 24 (74.60°, 52.31°, 53.09°)
- AD-B-B x 12 (83.43°, 48.29°, 48.29°)
- AE-B-C x 24 (86.14°, 45.82°, 48.03°)
- AE-E-J x 24 (80.57°, 48.01°, 51.42°)
- AF-H-L x 24 (78.24°, 49.42°, 52.34°)
- AF-I-U x 24 (75.32°, 49.28°, 55.40°)
- AG-E-K x 24 (82.20°, 47.22°, 50.58°)
- AG-H-R x 24 (77.79°, 48.31°, 53.90°)
- AH-N-S x 24 (75.30°, 51.28°, 53.42°)
- AH-O-Q x 24 (75.67°, 51.68°, 52.65°)
- AI-J-J x 8 (83.35°, 48.32°, 48.32°)
- AI-P-P x 8 (78.90°, 50.55°, 50.55°)
- AJ-J-J x 4 (83.41°, 48.30°, 48.30°)
- AJ-P-P x 4 (78.95°, 50.52°, 50.52°)
- AK-Q-W x 24 (76.41°, 50.16°, 53.42°)
- AL-S-X x 24 (76.41°, 50.54°, 53.04°)
- AL-T-U x 24 (77.75°, 51.01°, 51.24°)
- AM-P-R x 24 (80.50°, 49.28°, 50.22°)
- AM-T-V x 24 (77.47°, 50.22°, 52.31°)
- AN-Y-Y x 12 (77.54°, 51.23°, 51.23°)
- AO-W-Y x 24 (77.86°, 50.89°, 51.25°)
- AO-X-Z x 24 (77.48°, 50.88°, 51.64°)
- AP-V-V x 12 (78.88°, 50.56°, 50.56°)
- AP-Z-Z x 12 (77.55°, 51.23°, 51.23°)
- 30 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.995 or 49.75% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
7V Cube Dome Calculator
Geodesic 7V Cube Dome (Human is 170cm/5'7") |
The Cuboctahedron
  Cuboctahedron |
- Uniform Polyhedron: U7
- Archimedean Solid: A1
- Vertices: 12
- Edges: 24
- Faces: 14
- Wythoff symbol: 2|3 4
- Symmetry Group: octahedral
- Vertex Configuration: {3, 4, 3, 4}
- Dual: rhombic dodecahedron
- V: s3 * 5/3 * √2
- A: s2 * (6 + 2 * √3)
- rinner: s * 3/4
- router: s
Preparing the Cuboctahedron
1V/L1 Cuboctahedron Dome
|
|
|
- vertices/connectors: 12
- 9 x 4-way
- 3 x 6-way
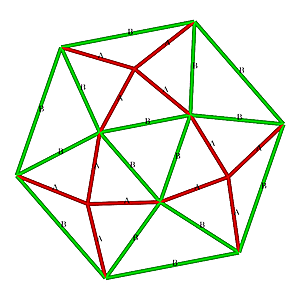
 1V Cuboctahedron Dome Construction Map
1V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 12: 0.76537 (22.50°)
- B x 15: 1.00000 (30.00°)
- total 27 struts (2 kinds)1)
- strut variance 30.7%
- faces: 16 (3-sided)
- A-A-B x 12 (49.21°, 49.21°, 81.57°)
- B-B-B x 4 (60.00°, 60.00°, 60.00°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.817 or 40.83% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
1V Cuboctahedron Dome Calculator
Geodesic 1V Cuboctahedron Dome (Human is 170cm/5'7") |
2V/L2 Cuboctahedron Dome
|
|
|
- vertices/connectors: 39
- 15 x 4-way
- 24 x 6-way
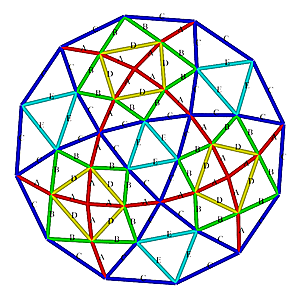
 2V Cuboctahedron Dome Construction Map
2V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 24: 0.39018 (11.25°)
- B x 24: 0.42291 (12.21°)
- C x 30: 0.51764 (15.00°)
- D x 12: 0.54120 (15.70°)
- E x 12: 0.57735 (16.78°)
- total 102 struts (5 kinds)1)
- strut variance 48.0%
- faces: 64 (3-sided)
- A-A-D x 12 (46.09°, 46.09°, 87.81°)
- A-B-C x 24 (47.72°, 53.31°, 78.96°)
- B-B-D x 12 (50.22°, 50.22°, 79.56°)
- C-C-E x 12 (56.10°, 56.10°, 67.80°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.943 or 47.15% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V Cuboctahedron Dome Calculator
Geodesic 2V Cuboctahedron Dome (Human is 170cm/5'7") |
There might be a better optimization available, but that's what I came up at the first sight.
3V Cuboctahedron Dome
|
|
|
- vertices/connectors: 82
- 21 x 4-way
- 61 x 6-way
 3V Cuboctahedron Dome Construction Map
3V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 24: 0.25480 (7.32°)
- B x 12: 0.27355 (7.86°)
- C x 24: 0.27468 (7.89°)
- D x 24: 0.27569 (7.92°)
- E x 24: 0.29082 (8.36°)
- F x 30: 0.33193 (9.55°)
- G x 12: 0.35741 (10.29°)
- H x 24: 0.36346 (10.47°)
- I x 27: 0.37796 (10.89°)
- J x 24: 0.38517 (11.10°)
- total 225 struts (10 kinds)1)
- strut variance 51.2%
- faces: 144 (3-sided)
- A-A-G x 12 (45.47°, 45.47°, 89.07°)
- A-D-F x 24 (48.51°, 54.14°, 77.35°)
- B-C-H x 24 (48.34°, 48.60°, 83.05°)
- C-C-G x 12 (49.42°, 49.42°, 81.16°)
- D-E-H x 24 (48.28°, 51.94°, 79.78°)
- E-E-I x 12 (49.46°, 49.46°, 81.07°)
- F-F-I x 12 (55.29°, 55.29°, 69.42°)
- I-J-J x 24 (58.77°, 60.62°, 60.62°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V Cuboctahedron Dome Calculator
Geodesic 3V Cuboctahedron Dome (Human is 170cm/5'7") |
4V Cuboctahedron Dome
|
|
|
- vertices/connectors: 141
- 27 x 4-way
- 114 x 6-way
 4V Cuboctahedron Dome Construction Map
4V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 24: 0.18820 (5.40°)
- B x 24: 0.20036 (5.75°)
- C x 24: 0.20240 (5.81°)
- D x 24: 0.20386 (5.85°)
- E x 24: 0.20571 (5.90°)
- F x 24: 0.21338 (6.12°)
- G x 24: 0.21629 (6.21°)
- H x 24: 0.21961 (6.30°)
- I x 30: 0.24197 (6.95°)
- J x 24: 0.26458 (7.60°)
- K x 12: 0.26497 (7.61°)
- L x 24: 0.27316 (7.85°)
- M x 24: 0.27685 (7.96°)
- N x 12: 0.27735 (7.97°)
- O x 30: 0.28011 (8.05°)
- P x 12: 0.28580 (8.22°)
- Q x 24: 0.29180 (8.39°)
- R x 12: 0.30151 (8.67°)
- total 396 struts (18 kinds)1)
- strut variance 60.2%
- faces: 256 (3-sided)
- A-A-K x 12 (45.25°, 45.25°, 89.50°)
- A-C-I x 24 (49.12°, 54.41°, 76.47°)
- B-B-K x 12 (48.61°, 48.61°, 82.78°)
- B-D-L x 24 (46.95°, 48.03°, 85.02°)
- C-F-J x 24 (48.66°, 52.34°, 78.99°)
- D-E-J x 24 (49.46°, 50.06°, 80.48°)
- E-G-L x 24 (47.98°, 51.37°, 80.65°)
- F-H-O x 24 (48.73°, 50.67°, 80.60°)
- G-G-P x 12 (48.65°, 48.65°, 82.70°)
- H-H-P x 12 (49.40°, 49.40°, 81.19°)
- I-I-N x 12 (55.04°, 55.04°, 69.91°)
- M-M-N x 12 (59.94°, 59.94°, 60.12°)
- M-O-Q x 24 (57.85°, 58.95°, 63.19°)
- Q-Q-R x 12 (58.89°, 58.89°, 62.21°)
- R-R-R x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.985 or 49.24% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
4V Cuboctahedron Dome Calculator
Geodesic 4V Cuboctahedron Dome (Human is 170cm/5'7") |
L3 Cuboctahedron Dome
|
|
|
- vertices/connectors: 141
- 27 x 4-way
- 114 x 6-way
 L3 Cuboctahedron Dome Construction Map
L3 Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 48: 0.19603 (5.62°)
- B x 24: 0.19991 (5.74°)
- C x 24: 0.20044 (5.75°)
- D x 48: 0.21266 (6.10°)
- E x 24: 0.21671 (6.22°)
- F x 24: 0.21746 (6.24°)
- G x 60: 0.26105 (7.50°)
- H x 24: 0.26433 (7.59°)
- I x 24: 0.26899 (7.73°)
- J x 24: 0.27316 (7.85°)
- K x 12: 0.27590 (7.93°)
- L x 12: 0.27686 (7.96°)
- M x 24: 0.29180 (8.39°)
- N x 12: 0.29886 (8.59°)
- O x 12: 0.30151 (8.67°)
- total 396 struts (15 kinds)1)
- strut variance 53.8%
- faces: 256 (3-sided)
- A-A-K x 12 (45.27°, 45.27°, 89.47°)
- A-B-J x 24 (45.78°, 46.96°, 87.27°)
- A-D-H x 24 (47.00°, 52.53°, 80.47°)
- A-E-G x 24 (47.32°, 54.37°, 78.32°)
- B-B-K x 12 (46.36°, 46.36°, 87.28°)
- C-D-G x 24 (48.74°, 52.92°, 78.34°)
- C-E-H x 24 (48.00°, 53.47°, 78.53°)
- D-D-L x 12 (49.39°, 49.39°, 81.22°)
- D-F-J x 24 (49.80°, 51.36°, 78.84°)
- F-F-L x 12 (50.46°, 50.46°, 79.07°)
- G-G-N x 12 (55.08°, 55.08°, 69.83°)
- G-I-M x 24 (55.32°, 57.91°, 66.78°)
- I-I-N x 12 (56.25°, 56.25°, 67.50°)
- M-M-O x 12 (58.89°, 58.89°, 62.21°)
- O-O-O x 4 (60.00°, 60.00°, 60.00°)
- 15 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.985 or 49.24% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 Cuboctahedron Dome Calculator
Geodesic L3 Cuboctahedron Dome (Human is 170cm/5'7") |
5V Cuboctahedron Dome
|
|
|
- vertices/connectors: 216
- 33 x 4-way
- 183 x 6-way
 5V Cuboctahedron Dome Construction Map
5V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 24: 0.14897 (4.27°)
- B x 24: 0.15701 (4.50°)
- C x 24: 0.15942 (4.57°)
- D x 24: 0.16077 (4.61°)
- E x 24: 0.16199 (4.65°)
- F x 24: 0.16287 (4.67°)
- G x 12: 0.16512 (4.74°)
- H x 24: 0.16655 (4.78°)
- I x 24: 0.16939 (4.86°)
- J x 24: 0.17295 (4.96°)
- K x 24: 0.17327 (4.97°)
- L x 24: 0.17393 (4.99°)
- M x 24: 0.17615 (5.05°)
- N x 30: 0.18984 (5.45°)
- O x 24: 0.20577 (5.91°)
- P x 12: 0.21009 (6.03°)
- Q x 24: 0.21329 (6.12°)
- R x 24: 0.21561 (6.19°)
- S x 24: 0.21702 (6.23°)
- T x 30: 0.21808 (6.26°)
- U x 12: 0.21822 (6.26°)
- V x 12: 0.22654 (6.50°)
- W x 24: 0.22702 (6.52°)
- X x 24: 0.22923 (6.58°)
- Y x 15: 0.22942 (6.59°)
- Z x 24: 0.23096 (6.63°)
- AA x 24: 0.23738 (6.82°)
- AB x 12: 0.24254 (6.97°)
- total 615 struts (28 kinds)1)
- strut variance 62.8%
- faces: 400 (3-sided)
- A-A-P x 12 (45.17°, 45.17°, 89.66°)
- A-C-N x 24 (49.58°, 54.54°, 75.88°)
- AA-AA-AB x 12 (59.29°, 59.29°, 61.43°)
- AA-X-Z x 24 (62.11°, 58.57°, 59.32°)
- AB-AB-AB x 4 (60.00°, 60.00°, 60.00°)
- B-B-P x 12 (48.00°, 48.00°, 84.00°)
- B-D-S x 24 (46.21°, 47.67°, 86.12°)
- C-H-O x 24 (49.32°, 52.43°, 78.26°)
- D-F-O x 24 (50.07°, 50.98°, 78.95°)
- E-G-R x 24 (48.15°, 49.39°, 82.46°)
- E-I-S x 24 (47.63°, 50.59°, 81.78°)
- F-J-R x 24 (48.05°, 52.12°, 79.83°)
- H-K-T x 24 (48.75°, 51.45°, 79.80°)
- I-I-V x 12 (48.05°, 48.05°, 83.91°)
- J-L-W x 24 (48.92°, 49.31°, 81.77°)
- K-M-W x 24 (48.94°, 50.06°, 81.00°)
- L-L-V x 12 (49.37°, 49.37°, 81.27°)
- M-M-Y x 12 (49.39°, 49.39°, 81.23°)
- N-N-U x 12 (54.91°, 54.91°, 70.17°)
- Q-Q-U x 12 (59.24°, 59.24°, 61.53°)
- Q-T-Z x 24 (56.62°, 58.64°, 64.74°)
- X-X-Y x 12 (59.97°, 59.97°, 60.06°)
- 22 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.990 or 49.51% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
5V Cuboctahedron Dome Calculator
Geodesic 5V Cuboctahedron Dome (Human is 170cm/5'7") |
6V Cuboctahedron Dome
|
|
|
- vertices/connectors: 307
- 39 x 4-way
- 268 x 6-way
 6V Cuboctahedron Dome Construction Map
6V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 24: 0.12319 (3.53°)
- B x 24: 0.12886 (3.69°)
- C x 24: 0.13134 (3.77°)
- D x 24: 0.13213 (3.79°)
- E x 24: 0.13294 (3.81°)
- F x 24: 0.13429 (3.85°)
- G x 24: 0.13485 (3.87°)
- H x 24: 0.13595 (3.90°)
- I x 24: 0.13710 (3.93°)
- J x 24: 0.13831 (3.97°)
- K x 24: 0.14205 (4.07°)
- L x 24: 0.14228 (4.08°)
- M x 24: 0.14239 (4.08°)
- N x 24: 0.14313 (4.10°)
- O x 24: 0.14372 (4.12°)
- P x 24: 0.14489 (4.15°)
- Q x 24: 0.14671 (4.21°)
- R x 24: 0.14719 (4.22°)
- S x 30: 0.15602 (4.47°)
- T x 24: 0.16762 (4.81°)
- U x 24: 0.17260 (4.95°)
- V x 12: 0.17389 (4.99°)
- W x 24: 0.17620 (5.05°)
- X x 30: 0.17706 (5.08°)
- Y x 24: 0.17943 (5.15°)
- Z x 12: 0.17961 (5.15°)
- AA x 24: 0.18035 (5.17°)
- AB x 24: 0.18541 (5.32°)
- AC x 24: 0.18597 (5.34°)
- AD x 12: 0.18657 (5.35°)
- AE x 24: 0.18878 (5.42°)
- AF x 54: 0.18984 (5.45°)
- AG x 12: 0.19220 (5.51°)
- AH x 48: 0.19238 (5.52°)
- AI x 24: 0.20000 (5.74°)
- AJ x 24: 0.20102 (5.77°)
- total 882 struts (36 kinds)1)
- strut variance 63.1%
- faces: 576 (3-sided)
- A-A-V x 12 (45.11°, 45.11°, 89.78°)
- A-C-S x 24 (49.88°, 54.59°, 75.53°)
- AA-E-I x 24 (83.83°, 47.09°, 49.08°)
- AA-G-N x 24 (80.90°, 47.55°, 51.56°)
- AB-K-P x 24 (80.47°, 49.10°, 50.42°)
- AB-L-O x 24 (80.82°, 49.26°, 49.92°)
- AC-AF-AH x 48 (58.24°, 60.18°, 61.58°)
- AD-J-J x 12 (84.85°, 47.58°, 47.58°)
- AD-M-M x 12 (81.87°, 49.07°, 49.07°)
- AE-M-N x 24 (82.80°, 48.44°, 48.76°)
- AE-O-Q x 24 (81.10°, 48.76°, 50.14°)
- AF-P-R x 24 (81.05°, 48.95°, 50.01°)
- AF-U-X x 24 (65.73°, 56.00°, 58.28°)
- AG-Q-Q x 12 (81.85°, 49.07°, 49.07°)
- AG-R-R x 12 (81.51°, 49.24°, 49.24°)
- AH-AH-AI x 24 (58.68°, 58.68°, 62.63°)
- AI-AJ-AJ x 24 (59.67°, 60.16°, 60.16°)
- B-B-V x 12 (47.58°, 47.58°, 84.84°)
- B-D-Y x 24 (45.84°, 47.33°, 86.83°)
- C-H-T x 24 (49.94°, 52.39°, 77.67°)
- D-F-T x 24 (50.43°, 51.60°, 77.97°)
- E-J-Y x 24 (47.30°, 49.89°, 82.80°)
- F-L-W x 24 (48.45°, 52.47°, 79.08°)
- G-I-W x 24 (49.04°, 50.18°, 80.78°)
- H-K-X x 24 (48.90°, 51.99°, 79.11°)
- S-S-Z x 12 (54.86°, 54.86°, 70.29°)
- U-U-Z x 12 (58.65°, 58.65°, 62.70°)
- 27 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
6V Cuboctahedron Dome Calculator
Geodesic 6V Cuboctahedron Dome (Human is 170cm/5'7") |
2V.3V Cuboctahedron Dome
|
|
|
- vertices/connectors: 307
- 39 x 4-way
- 268 x 6-way

 2V.3V Cuboctahedron Dome Construction Map
2V.3V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 48: 0.13005 (3.73°)
- B x 48: 0.13235 (3.79°)
- C x 24: 0.13239 (3.80°)
- D x 24: 0.13292 (3.81°)
- E x 24: 0.13301 (3.81°)
- F x 24: 0.13431 (3.85°)
- G x 24: 0.13456 (3.86°)
- H x 48: 0.14095 (4.04°)
- I x 24: 0.14363 (4.12°)
- J x 24: 0.14376 (4.12°)
- K x 24: 0.14386 (4.12°)
- L x 24: 0.14407 (4.13°)
- M x 24: 0.14420 (4.13°)
- N x 24: 0.14559 (4.17°)
- O x 24: 0.14602 (4.19°)
- P x 60: 0.17250 (4.95°)
- Q x 24: 0.17578 (5.04°)
- R x 24: 0.17622 (5.05°)
- S x 24: 0.17677 (5.07°)
- T x 30: 0.17792 (5.10°)
- U x 24: 0.17845 (5.12°)
- V x 24: 0.17859 (5.12°)
- W x 24: 0.18000 (5.16°)
- X x 24: 0.18035 (5.17°)
- Y x 12: 0.18353 (5.27°)
- Z x 12: 0.18409 (5.28°)
- AA x 24: 0.18431 (5.29°)
- AB x 24: 0.18489 (5.30°)
- AC x 12: 0.18657 (5.35°)
- AD x 24: 0.19238 (5.52°)
- AE x 12: 0.19845 (5.69°)
- AF x 24: 0.19944 (5.72°)
- AG x 24: 0.20000 (5.74°)
- AH x 24: 0.20102 (5.77°)
- total 882 struts (34 kinds)1)
- strut variance 54.6%
- faces: 576 (3-sided)
- A-A-Y x 12 (45.11°, 45.11°, 89.78°)
- A-C-X x 24 (46.02°, 47.12°, 86.86°)
- A-H-Q x 24 (46.89°, 52.30°, 80.82°)
- A-J-P x 24 (47.47°, 54.60°, 77.92°)
- AA-B-B x 24 (88.30°, 45.85°, 45.85°)
- AA-C-G x 24 (87.30°, 45.86°, 46.85°)
- AB-K-L x 24 (79.88°, 50.01°, 50.11°)
- AB-M-O x 24 (79.16°, 49.99°, 50.85°)
- AC-G-G x 12 (87.76°, 46.12°, 46.12°)
- AC-O-O x 12 (79.44°, 50.28°, 50.28°)
- AD-AD-AG x 12 (58.68°, 58.68°, 62.63°)
- AD-P-U x 24 (66.48°, 55.29°, 58.23°)
- AE-P-P x 12 (70.21°, 54.90°, 54.90°)
- AE-V-V x 12 (67.48°, 56.26°, 56.26°)
- AF-T-V x 24 (68.02°, 55.82°, 56.16°)
- AF-U-W x 24 (67.61°, 55.81°, 56.58°)
- AG-AH-AH x 24 (59.67°, 60.16°, 60.16°)
- AG-W-W x 12 (67.50°, 56.25°, 56.25°)
- B-B-Y x 12 (46.09°, 46.09°, 87.82°)
- B-I-R x 24 (47.54°, 53.20°, 79.26°)
- D-I-Q x 24 (47.88°, 53.27°, 78.86°)
- D-K-S x 24 (47.61°, 53.10°, 79.28°)
- E-H-P x 24 (48.96°, 53.03°, 78.01°)
- E-N-S x 24 (47.52°, 53.84°, 78.64°)
- F-J-R x 24 (48.33°, 53.12°, 78.55°)
- F-N-T x 24 (47.78°, 53.41°, 78.81°)
- H-H-Z x 12 (49.21°, 49.21°, 81.58°)
- H-M-X x 24 (49.94°, 51.56°, 78.50°)
- L-L-Z x 12 (50.30°, 50.30°, 79.40°)
- 29 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V.3V Cuboctahedron Dome Calculator
Geodesic 2V.3V Cuboctahedron Dome (Human is 170cm/5'7") |
3V.2V Cuboctahedron Dome
|
|
|
- vertices/connectors: 307
- 39 x 4-way
- 268 x 6-way
 3V.2V Cuboctahedron Dome Construction Map
3V.2V Cuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 48: 0.12766 (3.66°)
- B x 24: 0.12871 (3.69°)
- C x 24: 0.12884 (3.69°)
- D x 24: 0.13710 (3.93°)
- E x 48: 0.13767 (3.95°)
- F x 48: 0.13817 (3.96°)
- G x 24: 0.13839 (3.97°)
- H x 48: 0.13896 (3.98°)
- I x 24: 0.13926 (3.99°)
- J x 24: 0.13962 (4.00°)
- K x 48: 0.14580 (4.18°)
- L x 24: 0.14716 (4.22°)
- M x 24: 0.14733 (4.22°)
- N x 60: 0.16654 (4.78°)
- O x 24: 0.16744 (4.80°)
- P x 24: 0.16860 (4.84°)
- Q x 24: 0.17943 (5.15°)
- R x 12: 0.18017 (5.17°)
- S x 12: 0.18041 (5.18°)
- T x 48: 0.18249 (5.24°)
- U x 24: 0.18346 (5.26°)
- V x 24: 0.18358 (5.27°)
- W x 54: 0.18984 (5.45°)
- X x 12: 0.19101 (5.48°)
- Y x 12: 0.19164 (5.50°)
- Z x 24: 0.19259 (5.53°)
- AA x 48: 0.19350 (5.55°)
- AB x 48: 0.19619 (5.63°)
- total 882 struts (28 kinds)1)
- strut variance 53.6%
- faces: 576 (3-sided)
- A-A-R x 12 (45.13°, 45.13°, 89.75°)
- A-B-Q x 24 (45.37°, 45.83°, 88.80°)
- A-F-O x 24 (48.24°, 53.83°, 77.92°)
- A-I-N x 24 (48.36°, 54.61°, 77.02°)
- AA-AA-Z x 24 (60.15°, 60.15°, 59.69°)
- AA-AB-W x 48 (60.14°, 61.57°, 58.29°)
- AB-AB-Z x 24 (60.61°, 60.61°, 58.79°)
- B-B-R x 12 (45.57°, 45.57°, 88.87°)
- C-F-N x 24 (48.93°, 54.00°, 77.07°)
- C-I-O x 24 (48.61°, 54.23°, 77.17°)
- D-E-U x 24 (47.97°, 48.25°, 83.79°)
- D-H-T x 24 (48.18°, 49.07°, 82.75°)
- E-E-S x 12 (49.08°, 49.08°, 81.85°)
- E-G-T x 24 (48.46°, 48.79°, 82.75°)
- E-H-Q x 24 (49.27°, 49.90°, 80.83°)
- F-K-V x 24 (47.94°, 51.56°, 80.50°)
- F-L-T x 24 (48.11°, 52.46°, 79.43°)
- G-H-U x 24 (48.45°, 48.73°, 82.83°)
- H-H-S x 12 (49.54°, 49.54°, 80.92°)
- J-K-T x 24 (48.77°, 51.76°, 79.47°)
- J-L-V x 24 (48.40°, 52.04°, 79.56°)
- K-K-X x 12 (49.08°, 49.08°, 81.84°)
- K-M-W x 24 (49.30°, 49.99°, 80.71°)
- M-M-X x 12 (49.58°, 49.58°, 80.83°)
- N-N-Y x 12 (54.87°, 54.87°, 70.25°)
- N-P-W x 24 (54.98°, 56.02°, 69.00°)
- P-P-Y x 12 (55.37°, 55.37°, 69.25°)
- 27 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V.2V Cuboctahedron Dome Calculator
Geodesic 3V.2V Cuboctahedron Dome (Human is 170cm/5'7") |
The Truncated Octahedron
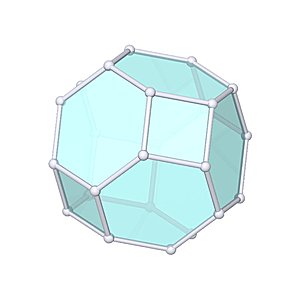  Truncated Octahedron |
- Uniform Polyhedron: U8
- Archimedean Solid: A12
- Vertices: 24
- Edges: 36
- Faces: 14
- Wythoff symbol: 2 4|3
- Symmetry Group: octahedral
- Vertex Configuration: {6, 6, 4}
- Dual: tetrakis hexahedron
- V: s3 * 8 * √2
- A: s2 * (6 + 12 * √3)
- rinner: s * 9/20 * √10
- router: s / 2 * √10
Preparing the Truncated Octahedron
1V/L1 Truncated Octahedron Dome
|
|
|
- vertices/connectors: 25
- 4 x 3-way
- 9 x 4-way
- 12 x 6-way
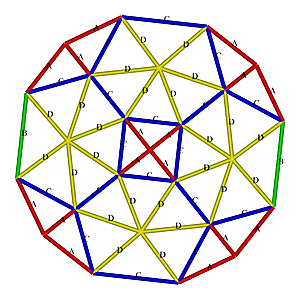
 1V Truncated Octahedron Dome Construction Map
1V Truncated Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 16: 0.45951 (13.28°)
- B x 2: 0.63245 (18.43°)
- C x 18: 0.63246 (18.44°)
- D x 24: 0.67142 (19.62°)
- total 60 struts (4 kinds)1)
- strut variance 46.1%
- faces: 36 (3-sided)
- A-A-C x 12 (46.51°, 46.51°, 86.98°)
- B-D-D x 2 (56.19°, 61.90°, 61.90°)
- C-D-D x 22 (56.20°, 61.90°, 61.90°)
- 3 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
1V Truncated Octahedron Dome Calculator
Geodesic 1V Truncated Octahedron Dome (Human is 170cm/5'7") |
2V/L2 Truncated Octahedron Dome
|
|
|
- vertices/connectors: 85
- 4 x 3-way
- 21 x 4-way
- 60 x 6-way
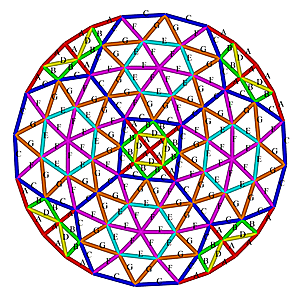
 2V Truncated Octahedron Dome Construction Map
2V Truncated Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.23131 (6.64°)
- B x 24: 0.23773 (6.83°)
- C x 40: 0.32036 (9.22°)
- D x 12: 0.32492 (9.35°)
- E x 24: 0.33571 (9.66°)
- F x 48: 0.34069 (9.81°)
- G x 48: 0.35506 (10.23°)
- total 228 struts (7 kinds)1)
- strut variance 53.5%
- faces: 144 (3-sided)
- A-A-D x 12 (45.39°, 45.39°, 89.23°)
- A-B-C x 24 (46.08°, 47.75°, 86.17°)
- B-B-D x 12 (46.89°, 46.89°, 86.22°)
- C-F-G x 48 (54.79°, 60.32°, 64.89°)
- E-F-F x 24 (59.03°, 60.48°, 60.48°)
- E-G-G x 24 (56.42°, 61.79°, 61.79°)
- 6 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V Truncated Octahedron Dome Calculator
Geodesic 2V Truncated Octahedron Dome (Human is 170cm/5'7") |
3V Truncated Octahedron Dome
|
|
|
- vertices/connectors: 181
- 4 x 3-way
- 33 x 4-way
- 144 x 6-way
 3V Truncated Octahedron Dome Construction Map
3V Truncated Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.15315 (4.39°)
- B x 16: 0.15689 (4.50°)
- C x 24: 0.15697 (4.50°)
- D x 24: 0.15706 (4.50°)
- E x 24: 0.16057 (4.60°)
- F x 40: 0.21070 (6.05°)
- G x 12: 0.21595 (6.20°)
- H x 24: 0.21723 (6.24°)
- I x 20: 0.22086 (6.34°)
- J x 24: 0.22224 (6.38°)
- K x 96: 0.22365 (6.42°)
- L x 48: 0.23512 (6.75°)
- M x 24: 0.23594 (6.77°)
- N x 48: 0.23610 (6.78°)
- O x 48: 0.23760 (6.82°)
- total 504 struts (15 kinds)1)
- strut variance 55.1%
- faces: 324 (3-sided)
- A-A-G x 12 (45.17°, 45.17°, 89.65°)
- A-D-F x 24 (46.46°, 48.02°, 85.52°)
- B-C-H x 24 (46.20°, 46.24°, 87.57°)
- C-C-G x 12 (46.54°, 46.54°, 86.93°)
- D-E-H x 24 (46.20°, 47.55°, 86.25°)
- E-E-I x 12 (46.55°, 46.55°, 86.90°)
- F-K-L x 48 (54.62°, 59.91°, 65.47°)
- I-N-N x 24 (55.78°, 62.11°, 62.11°)
- J-K-K x 24 (59.59°, 60.21°, 60.21°)
- J-O-O x 24 (55.76°, 62.12°, 62.12°)
- K-L-N x 48 (56.66°, 61.45°, 61.90°)
- K-M-O x 48 (56.36°, 61.44°, 62.21°)
- 12 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V Truncated Octahedron Dome Calculator
Geodesic 3V Truncated Octahedron Dome (Human is 170cm/5'7") |
4V Truncated Octahedron Dome
|
|
|
- vertices/connectors: 313
- 4 x 3-way
- 45 x 4-way
- 264 x 6-way
 4V Truncated Octahedron Dome Construction Map
4V Truncated Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 32: 0.11427 (3.28°)
- B x 24: 0.11666 (3.34°)
- C x 24: 0.11683 (3.35°)
- D x 32: 0.11742 (3.37°)
- E x 24: 0.11755 (3.37°)
- F x 24: 0.11965 (3.43°)
- G x 24: 0.11984 (3.44°)
- H x 24: 0.12061 (3.46°)
- I x 40: 0.15644 (4.49°)
- J x 36: 0.16131 (4.63°)
- K x 24: 0.16300 (4.67°)
- L x 40: 0.16496 (4.73°)
- M x 48: 0.16522 (4.74°)
- N x 24: 0.16525 (4.74°)
- O x 12: 0.16571 (4.75°)
- P x 48: 0.16582 (4.76°)
- Q x 48: 0.16845 (4.83°)
- R x 24: 0.16996 (4.87°)
- S x 48: 0.17431 (5.00°)
- T x 48: 0.17490 (5.02°)
- U x 48: 0.17555 (5.04°)
- V x 48: 0.17612 (5.05°)
- W x 48: 0.17760 (5.09°)
- X x 48: 0.17888 (5.13°)
- Y x 48: 0.18059 (5.18°)
- total 888 struts (25 kinds)1)
- strut variance 58.0%
- faces: 576 (3-sided)
- A-A-J x 12 (45.12°, 45.12°, 89.76°)
- A-C-I x 24 (46.74°, 48.09°, 85.18°)
- B-B-J x 12 (46.28°, 46.28°, 87.43°)
- B-D-K x 24 (45.69°, 46.05°, 88.26°)
- C-F-J x 24 (46.25°, 47.76°, 86.00°)
- D-E-J x 24 (46.60°, 46.71°, 86.69°)
- E-G-K x 24 (46.08°, 47.20°, 86.72°)
- F-H-L x 24 (46.41°, 46.86°, 86.73°)
- G-G-O x 12 (46.25°, 46.25°, 87.51°)
- H-H-O x 12 (46.61°, 46.61°, 86.78°)
- I-P-T x 48 (54.57°, 59.75°, 65.68°)
- L-S-W x 48 (55.91°, 61.03°, 63.06°)
- M-S-T x 48 (56.47°, 61.58°, 61.95°)
- M-V-X x 48 (55.46°, 61.41°, 63.13°)
- N-P-P x 24 (59.80°, 60.10°, 60.10°)
- N-U-U x 24 (56.16°, 61.92°, 61.92°)
- Q-U-V x 48 (57.22°, 61.24°, 61.54°)
- Q-X-Y x 48 (55.86°, 61.56°, 62.58°)
- R-W-W x 24 (57.19°, 61.41°, 61.41°)
- R-Y-Y x 24 (56.15°, 61.92°, 61.92°)
- 20 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
4V Truncated Octahedron Dome Calculator
Geodesic 4V Truncated Octahedron Dome (Human is 170cm/5'7") |
L3 Truncated Octahedron Dome
|
|
|
- vertices/connectors: 313
- 4 x 3-way
- 45 x 4-way
- 264 x 6-way
 L3 Truncated Octahedron Dome Construction Map
L3 Truncated Octahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 64: 0.11585 (3.32°)
- B x 24: 0.11663 (3.34°)
- C x 24: 0.11667 (3.34°)
- D x 48: 0.11908 (3.41°)
- E x 48: 0.11988 (3.44°)
- F x 80: 0.16070 (4.61°)
- G x 24: 0.16129 (4.63°)
- H x 48: 0.16266 (4.67°)
- I x 24: 0.16300 (4.67°)
- J x 24: 0.16362 (4.69°)
- K x 48: 0.16845 (4.83°)
- L x 6: 0.17034 (4.89°)
- M x 18: 0.17035 (4.89°)
- N x 24: 0.17056 (4.89°)
- O x 96: 0.17097 (4.90°)
- P x 96: 0.17281 (4.96°)
- Q x 96: 0.17824 (5.11°)
- R x 48: 0.18000 (5.16°)
- S x 48: 0.18023 (5.17°)
- total 888 struts (19 kinds)1)
- strut variance 55.6%
- faces: 576 (3-sided)
- A-A-J x 12 (45.06°, 45.06°, 89.88°)
- A-B-I x 24 (45.26°, 45.66°, 89.07°)
- A-D-G x 24 (45.79°, 47.49°, 86.72°)
- A-E-F x 24 (45.96°, 48.09°, 85.95°)
- B-B-J x 12 (45.45°, 45.45°, 89.10°)
- C-D-F x 24 (46.42°, 47.67°, 85.92°)
- C-E-G x 24 (46.19°, 47.86°, 85.95°)
- D-D-J x 12 (46.62°, 46.62°, 86.76°)
- D-E-I x 24 (46.79°, 47.21°, 86.00°)
- E-E-J x 12 (46.98°, 46.98°, 86.04°)
- F-O-R x 48 (54.42°, 59.93°, 65.64°)
- F-P-Q x 48 (54.47°, 61.05°, 64.48°)
- H-O-Q x 48 (55.49°, 60.01°, 64.50°)
- H-P-R x 48 (54.88°, 60.31°, 64.81°)
- K-O-P x 48 (58.65°, 60.14°, 61.21°)
- K-Q-S x 48 (56.05°, 61.38°, 62.58°)
- L-O-O x 6 (59.73°, 60.14°, 60.14°)
- L-P-P x 6 (59.05°, 60.48°, 60.48°)
- M-O-O x 18 (59.77°, 60.12°, 60.12°)
- M-P-P x 18 (59.08°, 60.46°, 60.46°)
- N-Q-Q x 24 (57.20°, 61.40°, 61.40°)
- N-S-S x 24 (56.51°, 61.75°, 61.75°)
- 22 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.000 or 50.00% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
L3 Truncated Octahedron Dome Calculator
Geodesic L3 Truncated Octahedron Dome (Human is 170cm/5'7") |
The Rhombicuboctahedron
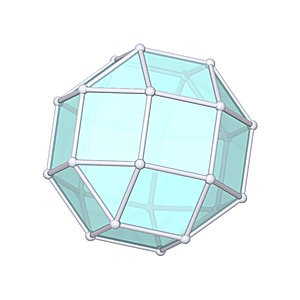  Rhombicuboctahedron |
- Uniform Polyhedron: U10
- aka Small Rhombicuboctahedron
- Archimedean Solid: A6
- Vertices: 24
- Edges: 48
- Faces: 26
- Wythoff symbol: 3 4|2
- Symmetry Group: octahedral
- Vertex Configuration: {4, 3, 4, 4}
- Dual: deltoidal icositetrahedron
- V: s3 / 3 * (12 + 10 * √2)
- A: s2 * (18 + 2 * √3)
- rinner: s / 17 * (6 + √2) * √(5 + 2 * √2)
- router: s / 2 * √(5 + 2 * √2)
Preparing the Rhombicuboctahedron
1V/L1 3/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 17
- 13 x 4-way
- 4 x 7-way
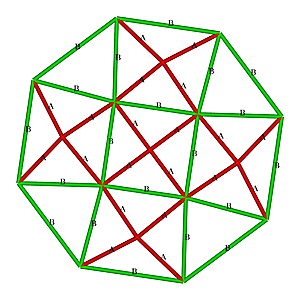
 1V 3/8 Rhombicuboctahedron Dome Construction Map
1V 3/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 20: 0.52372 (15.18°)
- B x 20: 0.71481 (20.94°)
- total 40 struts (2 kinds)1)
- strut variance 36.5%
- faces: 24 (3-sided)
- A-A-B x 20 (46.96°, 46.96°, 86.07°)
- B-B-B x 4 (60.00°, 60.00°, 60.00°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.643 or 32.14% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
1V 3/8 Rhombicuboctahedron Dome Calculator
Geodesic 1V 3/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
1V/L1 5/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 33
- 13 x 4-way
- 8 x 5-way
- 12 x 7-way
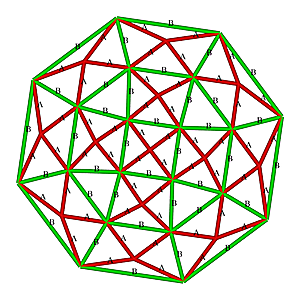
 1V 5/8 Rhombicuboctahedron Dome Construction Map
1V 5/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 52: 0.52372 (15.18°)
- B x 36: 0.71481 (20.94°)
- total 88 struts (2 kinds)1)
- strut variance 36.5%
- faces: 56 (3-sided)
- A-A-B x 52 (46.96°, 46.96°, 86.07°)
- B-B-B x 4 (60.00°, 60.00°, 60.00°)
- 2 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.358 or 67.88% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
1V 5/8 Rhombicuboctahedron Dome Calculator
Geodesic 1V 5/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
This is a nice variant, with square walls, optionally instead of square triangulation either replaced by one strut (B * √2) or leave it out at all.
The vertical struts of the vertical wall make it look very artistic, yet also edgy, but given it's a 1V it's understandable. With only 88 struts you get a 5/8 sphere.
At d = 6m the height is apprx. 4m and a 2nd level can be done at 2m height, just at the level of existing connectors.
2V/L2 3/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 57
- 21 x 4-way
- 32 x 6-way
- 4 x 7-way
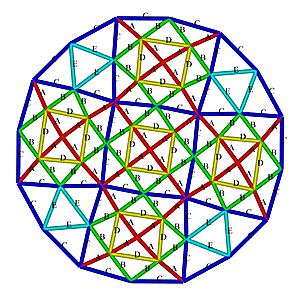
 2V 3/8 Rhombicuboctahedron Dome Construction Map
2V 3/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 40: 0.26418 (7.59°)
- B x 40: 0.27386 (7.87°)
- C x 40: 0.36346 (10.47°)
- D x 20: 0.37033 (10.67°)
- E x 12: 0.38268 (11.03°)
- total 152 struts (5 kinds)1)
- strut variance 44.9%
- faces: 96 (3-sided)
- A-A-D x 20 (45.51°, 45.51°, 88.98°)
- A-B-C x 40 (46.39°, 48.64°, 84.97°)
- B-B-D x 20 (47.47°, 47.47°, 85.06°)
- C-C-E x 12 (58.24°, 58.24°, 63.53°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.643 or 32.14% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V 3/8 Rhombicuboctahedron Dome Calculator
Geodesic 2V 3/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
2V/L2 5/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 121
- 21 x 4-way
- 8 x 5-way
- 80 x 6-way
- 12 x 7-way
 2V 5/8 Rhombicuboctahedron Dome Construction Map
2V 5/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 104: 0.26418 (7.59°)
- B x 104: 0.27386 (7.87°)
- C x 72: 0.36346 (10.47°)
- D x 52: 0.37033 (10.67°)
- E x 12: 0.38268 (11.03°)
- total 344 struts (5 kinds)1)
- strut variance 44.9%
- faces: 224 (3-sided)
- A-A-D x 52 (45.51°, 45.51°, 88.98°)
- A-B-C x 104 (46.39°, 48.64°, 84.97°)
- B-B-D x 52 (47.47°, 47.47°, 85.06°)
- C-C-E x 12 (58.24°, 58.24°, 63.53°)
- E-E-E x 4 (60.00°, 60.00°, 60.00°)
- 5 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.383 or 69.14% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
2V 5/8 Rhombicuboctahedron Dome Calculator
Geodesic 2V 5/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
This is also a nice variant, alike the 1V 5/8 one. Multiple squares in a spherical setting, a nice crossover of rectangular to circular/spherical space.
With 344 struts still considerable for temporary buildings.
3V 3/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 121
- 29 x 4-way
- 88 x 6-way
- 4 x 7-way
 3V 3/8 Rhombicuboctahedron Dome Construction Map
3V 3/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 40: 0.17453 (5.01°)
- B x 20: 0.18015 (5.17°)
- C x 40: 0.18031 (5.17°)
- D x 40: 0.18048 (5.18°)
- E x 40: 0.18562 (5.33°)
- F x 40: 0.23805 (6.84°)
- G x 20: 0.24588 (7.06°)
- H x 40: 0.24779 (7.12°)
- I x 32: 0.25307 (7.27°)
- J x 24: 0.25516 (7.33°)
- total 336 struts (10 kinds)1)
- strut variance 46.2%
- faces: 216 (3-sided)
- A-A-G x 20 (45.20°, 45.20°, 89.59°)
- A-D-F x 40 (46.82°, 48.96°, 84.22°)
- B-C-H x 40 (46.56°, 46.59°, 86.85°)
- C-C-G x 20 (47.01°, 47.01°, 85.99°)
- D-E-H x 40 (46.54°, 48.28°, 85.19°)
- E-E-I x 20 (47.01°, 47.01°, 85.98°)
- F-F-I x 12 (57.89°, 57.89°, 64.21°)
- I-J-J x 24 (59.46°, 60.27°, 60.27°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 0.643 or 32.14% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V 3/8 Rhombicuboctahedron Dome Calculator
Geodesic 3V 3/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
3V 5/8 Rhombicuboctahedron Dome
|
|
|
- vertices/connectors: 265
- 29 x 4-way
- 8 x 5-way
- 216 x 6-way
- 12 x 7-way
 3V 5/8 Rhombicuboctahedron Dome Construction Map
3V 5/8 Rhombicuboctahedron Dome Construction Map- edges/struts & bending angles (αstrut):
- A x 104: 0.17453 (5.01°)
- B x 52: 0.18015 (5.17°)
- C x 104: 0.18031 (5.17°)
- D x 104: 0.18048 (5.18°)
- E x 104: 0.18562 (5.33°)
- F x 72: 0.23805 (6.84°)
- G x 52: 0.24588 (7.06°)
- H x 104: 0.24779 (7.12°)
- I x 48: 0.25307 (7.27°)
- J x 24: 0.25516 (7.33°)
- total 768 struts (10 kinds)1)
- strut variance 46.2%
- faces: 504 (3-sided)
- A-A-G x 52 (45.20°, 45.20°, 89.59°)
- A-D-F x 104 (46.82°, 48.96°, 84.22°)
- B-C-H x 104 (46.56°, 46.59°, 86.85°)
- C-C-G x 52 (47.01°, 47.01°, 85.99°)
- D-E-H x 104 (46.54°, 48.28°, 85.19°)
- E-E-I x 52 (47.01°, 47.01°, 85.98°)
- F-F-I x 12 (57.89°, 57.89°, 64.21°)
- I-J-J x 24 (59.46°, 60.27°, 60.27°)
- 8 kinds of faces2)
- diameter: 2.000, radius: 1.000
- height: 1.380 or 68.99% of diameter
1) strut lengths sorted by 1/10'000th or +/-0.00005 exact
2) clock wise (cw) and counter clock wise (ccw) orientation neglected
3V 5/8 Rhombicuboctahedron Dome Calculator
Geodesic 3V 5/8 Rhombicuboctahedron Dome (Human is 170cm/5'7") |
Building Models
Building a model I think is very useful, you are getting an impression of the overall overhead, struts, connectors and even sewing the cover. Yet, a model cannot replace thorough investigation of the actual method and construction; I tend to make small tests in actual size for critical parts of a construction.
Anyway, I made a couple of geodesic models, four of them I include here in more details.
Please note, the notion of the strut types (lengths) A-F for 2V, 3V and the 4V Icosahedron models do not match the ones I listed previously, the strut notion for the models are those from DesertDomes.com  which I used in previous version of these notes.
In case you also used a different notion, you can easily map them to my notion, just compare the values, they are numerically the same, just the notion of A, B, C etc are different.
which I used in previous version of these notes.
In case you also used a different notion, you can easily map them to my notion, just compare the values, they are numerically the same, just the notion of A, B, C etc are different.
3V 5/9 Icosahedron Model
  3V 5/9 Dome, build with bamboo sticks and PVC pipe as junction |
So, I bought
- 150 bamboo sticks (10 packages a 15 sticks), 4mm diameter, 40cm long, and
- 9m PVC pipe outer diameter 6mm, inner diameter 4mm
Cost CHF 18, € 12 or US$15. I used the 3V 5/9 calculator entered Alath+Blath+Clath = 40cm, and lhole = 0.5cm, and got my Alath, Blath and Clath to cut.
- r = 37cm, d = 74cm
- A = 11.9cm (x 60)
- B = 13.9cm (x 90)
- C = 14.2cm (x 120)
so I actually cut for a full sphere, whereas the 3V 5/9 sphere only requires A x 30, B x 55, C x 80. Following cuts I made:
- 90x B+C
- 30x A+C
- 15x A+A
Step by Step
2V Icosahedron Model
As considered I used the left-over of the 3V and some spare sticks to build a 2V 4/8 Sphere:
- r = 18.3cm, d = 36.6cm
- A = 11.4cm (x 35)
- B = 10.0cm (x 30)
It has been quite some fun to build these two models, and also sense the stability within the dome while building it.
4V Icosahedron Model
  4V 4/8 Dome |
- r = 32cm, d = 64cm
- A = 8.0cm (x 30)
- B = 9.4cm (x 30)
- C = 9.4cm (x 60)
- D = 10.0cm (x 70)
- E = 10.4cm (x 30)
- F = 9.5cm (x 30)
So, B, C and F are very close, and since cutting so small bamboo so exact is hardly possible for me I made them all the same.
The D and E I marked with color to distinct them.
  4V 4/8 Dome (Closeup) |
- 60x C+D
- 5x D+D
- 30x A+E
- 30x B+F
Step by Step
The 4V 4/8 dome came out very well, the 4mm pipe isn't narrow enough for the bamboo thereby the dome isn't as stable, e.g. when moving around. It would be better to have actually 1mm less diameter of the inner diameter of the pipe than the thickness of the sticks. So far, the 4V looks more filigree than the 3V I think, less edgy, obvious due higher subdivision.
2V/L2 Cuboctahedron Model
|
|
|
|
|
- Vertices/Connectors: 39
- 15 x 4-way
- 24 x 6-way
- Faces: 64 (3-sided)
- Edges/Struts:
- A x 24: 0.39018
- B x 24: 0.42291
- C x 30: 0.51764
- D x 12: 0.54120
- E x 12: 0.57735
- total 102 struts (5 kinds)
- strut variance 47.9%
- diameter: 2.000, radius: 1.000
- height: 0.943 or 47.15% of diameter
So I optimize:
- 12 x (A + E) = 1.0
- 12 x (A + D)
- 24 x (B + C)
- 6 x C
- total 54 laths
- (A+E) = 1.0, therefore
- A = 0.403, B = 0.436, C = 0.534, D = 0.559, E = 0.596
- (Alath+Elath) = ~20cm (using 27 x 40cm bamboo equal 54 x 20cm bamboo)
- lhole = 0.75cm, Alath = 7.5cm, Blath = 8.3cm, Clath = 10.6cm, Dlath = 11.1cm, Elath = 11.9cm
I first calculated A+E (instead of Alath+Elath) which made the struts 0.5cm longer A and B, for C, D and E the error was neglectable, but the resulting dome looked strange, until I realized those 0.75cm do really matter at that scale of the model. So I recommend using lhole even you are doing a model at 10cm scale or so.
Real Life Application
I considered the geodesic dome for doing a temporary building or habitat. Using a set of struts, build by wooden roof laths (very cheap and easy to get here in Switzerland), and building a 5-6m diameter dome for myself to live in it. I merely doing the skeleton of the dome (no faces), and put then a cover over it (shape not yet determined).
Options
Following options for a shelter are considered for me, I target diameter from 6m to 8m, for now I focused only on the Icosahedron based domes:
  2V 4/8 Icosahedron Dome |
- llath 3m long lath (A+B)
- 5.62m diameter
- 35 laths
For my personal taste it's too edgy, and won't really consider it.
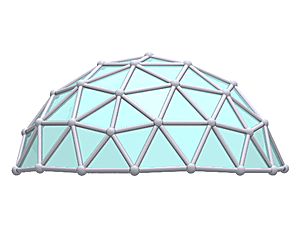  3V 4/9 Icosahedron Dome |
- 5.39m diameter
- llath 2m long lath (B+C)
- 60 laths
This option looks better, and I have been pondering on it with an additional wall, e.g. lattice wall from the yurt, yet the stability of the wall in this case isn't secured.
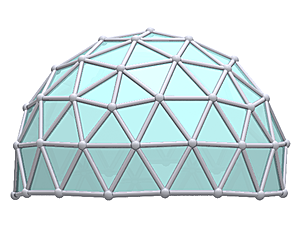  3V 5/9 Icosahedron Dome |
- 6.13m diameter
- llath 2.5m long lath (B+C)
- 83 laths
Very good head space, yet, the base line isn't straight, and some levelers are required.
  4V 4/8 Icosahedron Dome |
- 6.3m diameter, llath 1.82m (D+D) bamboo with lhole 2-3cm
- with total height of 3.1m it would be optionally to make another level, e.g. at 1.8m height for beds
- 7.10m diameter, llath 2.10m (D+D) bamboo with lhole 2-3cm
- with total height of 3.65m it would be suitable to make another level, at 2m height.
- 8.05m diameter, llath 2.40m (D+D) bamboo with lhole 2-3cm
- with total height of 4m it would be very obvious to make another level, at 2m height.
- 125 laths
This I personally consider most nice as it's more smooth and less edgy, yet, the overhead for 250 struts becomes significantly now.
In late winter/spring 2007 I started to build a 6.3m diameter 4V 4/8 dome with bamboo struts, consider to read my diary.
Connectors
 Strut Connector |
With screws for wood and M10 screw the total cost per strut is about CHF 2.10 - 3.00, which brings the cost quite up, e.g. 4V 4/8 dome 7m diameter costs about CHF 510 or € 330.
Thinking of using bamboo (with variable diameter naturally) is another option, costs apprx. CHF 0.35 per 182cm bamboo (@250 pieces) from a wholesale garden company.
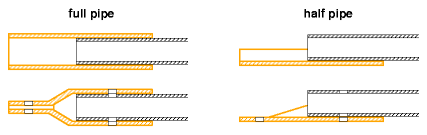 Pipe Connector |
In case of round profile struts (such as bamboo) another approach is to use a soft pipe as connector, like LD-PE and squeeze the one end. For variable diameter such as bamboo (or everything naturally grown) the half pipe is more suitable, adapting to variable diameter, using cable binder like this:
The estimated costs are low, for half-pipe only few cents, and one screw per connection (not strut) plus the cable binder also a few cents. This approach with a LDPE pipe is suitable for lightweight tent-like setups, not recommended when the dome is covered with solid cardboard or alike.
Separate Functions
Some dome critics describe the problems to insulate the dome because of the many junctions and seams. An architect who worked on domes recommended to me to separate the functions:
- static
- thermal insulation
- water/weather insulation
then each part can be secured individually.
The problem only arises when all functions are targeted to be resolved with one solution, e.g. the static also must provide also water insulation and this is difficult.
Since I focus on "temporary buildings", buildings which can be put up and taken down within a short period of time such as 2-3 hours, this has to be kept in mind.
Cover
 |
- water-resistant fabric stripes/leaf-like segments over the dome: cheap fabric, but might such cover hides the beauty of the dome then outside.
- wood or cardboard triangle faces to cover entire dome, and use shingles to protects against rain leaking the many strut junction, but this would run against "temporary" building as it wouldn't be such one anymore.
So, the synthetic fabric for the cover seems my option, yet, the beauty of the architecture is covered and vanishes; also a complicated folding or sew pattern is required to have the cover fit closely.
If I use a rectangular blanket, then I require d * π / 2 side length.
4/8 Sphere Cover Calculator
This approach provides leaf-like composition to have a half-sphere roof canvas.
Symbols & Formulas:
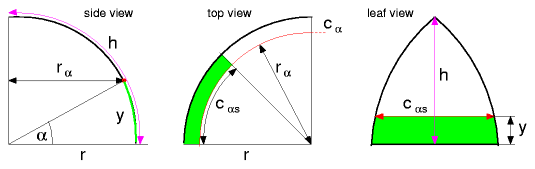 |
| α = 0 .. 90° | cα = rα * 2 * π | h = r * 2 * π / 4 |
| rα = cos( α ) * r | cαs = cα / nleaves | y = h * ( α / 90 ) |
Edit the diameter d, and amount of segments nleaves, and the canvas lanes wide wcanvas which is used to patch together a leaf, and then press "calculate".
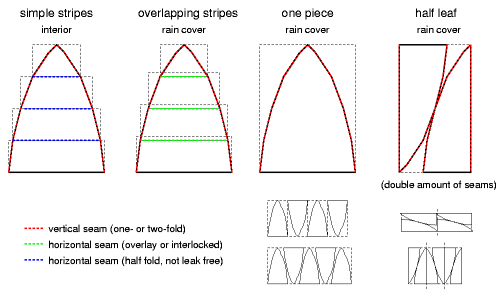 Leaf composition: interior & rain canvas |
Note: Since the calculator for now provides just 4/8 cover, I recommend:
- 4/9 sphere: reduce it accordingly at the bottom
- 5/9 sphere: add rectangular lane/stripe, in which you sew a cord which is used to make the bottom of the 1/9 of a 5/9 sphere fit closely (with wrinkels)
If you made experiences yourself with 5/9 sphere with leaf-like cover approach, drop me an email.
Sewing the Cover
In order to sew these leaf-like sphere surface together as rain cover, the water leak is particular to be avoided and so special care of how to sew the seams together:
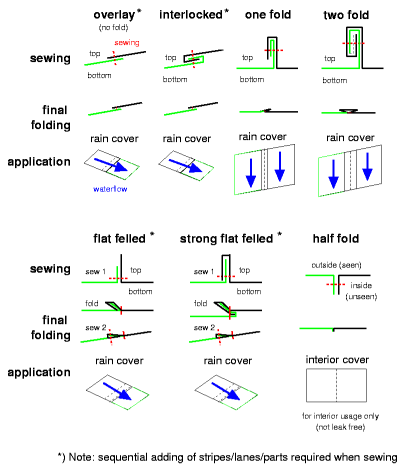 Options of Seam Sewing |
In case of the wigwam a combination of two of the options might be used:
- overlay horizontal canvas stripes or lanes to compose a part of a roof leaf or segment
- use either one-fold or two-fold to patch the leaves / segments together
Consider to seal the stitching holes from sewing with silicon or good clear tape for canvas (with threads) and preferable use water-resistant sewing thread as well.
4V 4/8 Geodesic Dome Model with Cover
  4V 4/8 Geodesic Dome with leaf-like segment composed cover |
Step by step of the making of:
As I experienced with this test for the 4V model, the top ending is hard to sew as the "two fold" seam is moderately thick, but overlaying 6 of them is too hard to sew, therefore I did leave it open. For a real life application a (clear) top cover would be build, e.g. a frame along the "top" 5 sided polygon of the 4V dome to hold the top cover.
Maybe I will extend the 4V Model further and test some ideas, let's see.
Windows & Door
A special consideration is the door, the triangle usually are too small to climb in (such as in case of a 3V 5/8), so a special strut combination might be use to extend a location to become the door, still triangular but large enough so one can enter the dome.
For now I consider to make the top most strut star covered by transparent plastic, and overlap the other cover, maybe use a four cords to fix the (square) sky cover, like in case of a yurt. Additional windows I will consider, but not yet sure about the weather/rain insulation of such. See my diary for the decision I actually made meanwhile.
Interior & Floor
Alike a yurt I will put a bright interior cotton cover as first layer, this way the construction is seen from the inside. Additionally putting in a wooden floor composed by laths or larger wooden plates.
 Floor Examples |
2nd Floor
With high ceiling making a 2nd floor for beds is an interesting option, in particular in the winter-time when the heat from the stove rises.
  2nd Floor Options in Dome |
- "1/4 moon": 2 pieces and 5 columns, best light distribution from the skylight.
- "3/4 moon": 1 or 2 pieces, 4 columns
- "4/4 moon": 1-4 pieces, 4 columns
- "eclipse": 1 or 4 pieces, 4+ columns, the light from the skylight reaches both levels, the 2nd floor and also the base.
Links
- Desert Domes: Tips

- Worldflower Garden Dome.com
 , vast site with many variants
, vast site with many variants
- PacificDomes.com
 , wonderful geodesic domes with tent-like setup
, wonderful geodesic domes with tent-like setup
- Red Sky Shelters
 , 1V based tents called "Yome"
, 1V based tents called "Yome"