Home   ·   About   ·   Tipi   ·   Yurt / Ger   ·   Dome   ·   Features   ·   Gallery About Overview License Tipi Overview Tipi Diary Yurt / Ger Overview Yurt Notes & Calculator Yurt / Ger Diary Yurt Builder Conference Living Notes Material Notes Dome Overview Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Features Overview Chris Aeppli Claudius Kern René K. Müller Geodesic Solitude Johnny's Capsule Geodesic Clay Mud Dome Jurtendorf (Switzerland) Neolithics of Pfyn Strawbale Cabin Dome Geodesic Dome Geodesic Dome Notes & Calculator Geodesic Dome Diary Geodesic Polyhedra Polyhedra Notes Introduction Platonic Solids Archimedean Solids Johnson Solids Uniform Polyhedra Waterman Polyhedra Bow Dome Triangulated Bow Dome Star Dome Star Dome Diary Wigwam Zome Helix Zome Low Cost Dome (PVC) Miscellaneous Domes Site Search Enter term & press ENTER If you found the information useful, consider to make a donation:   Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Next >> Polyhedra Notes written by Rene K. Mueller, Copyright (c) 2007, last updated Wed, January 9, 2008 Waterman Polyhedra Waterman polyhedra exist in mathematics since about 1990, a rather recent discovery. The concept of Waterman polyhedra was developed by Steve Waterman and relate to "Cubic Close Packing" (CCP) of spheres, also known as IVM (Isotropic Vector Matrix) by R. Buckminster Fuller. 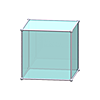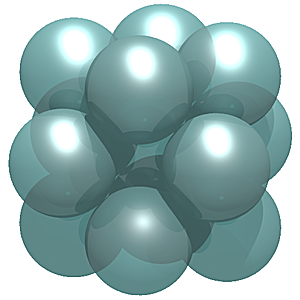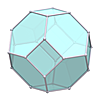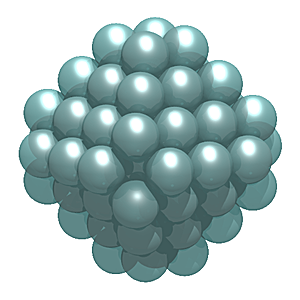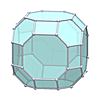Spheres are packed in a cubic manner: x, y and z are integers, sphere diameter is √2 thereby, at 0,0,0 resides the first sphere, and then those removed which have longer vector than √(2*n) from the center (0,0,0) and then a convex hull is calculated which gives a polyhedron: Waterman W24 O1 (radius √48) Waterman W24 O1 Some More Examples Waterman W1 O1 (radius √2) Waterman W5 O1 (radius √10) Waterman W24 O1 (radius √48) 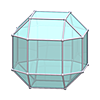Waterman W200 O1 (radius √400) Waterman W1000 O1 (radius √2000) 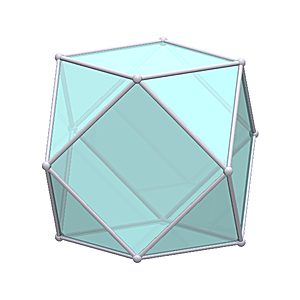Waterman W1 O1 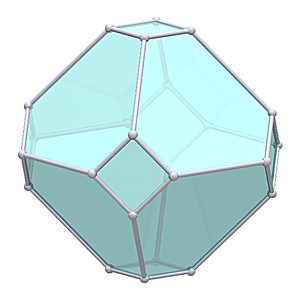Waterman W5 O1 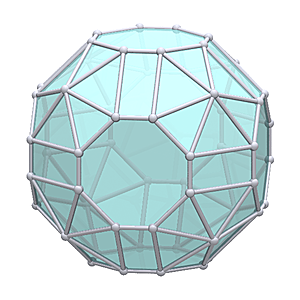Waterman W24 O1 Waterman W200 O1 Waterman W1000 O1 Different Origins Several origins are available as summarized by Mirek Majewski : Origin Origin Location radius Comment 1 0,0,0 √(2*n) Atom center: traditional origin of Waterman polyhedra, symmetry properties of a cube. 2 1/2,1/2,0 √(2+4*n)/2 Touch point between 2 atoms: symmetry properties of flat rectangle whose top & bottom faces are the same 3 1/3,1/3,2/3 √(6*(n+1))/3 Void center between 3 atoms: symmetry properties of flat triangle whose top & bottom faces are different 3* 1/3,1/3,1/3 √(3+6*n)/3 Void center between 3 lattice voids: same symmetry of origin 3. 4 1/2,1/2,1/2 √(3+8*(n-1))/2 Tretrahedron void center between 4 atoms: symmetry properties of a tetrahedron. 5 0,0,1/2 √(1+4*n)/2 5 atoms: symmetry properties of a flat rectangle whose top & bottom are different. 6 1,0,0 √(1+2*(n-1)) Octahedral void center between 6 atoms: symmetry properties of a cube. 7 Origins of Waterman Polyhedra by Mark Newbold whereas n starts with 1 for all origins. O1 O2 O3 O3* O4 O5 O6 W1 W2 W3 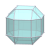W4 W5 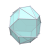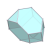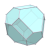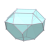W6 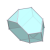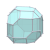W7 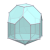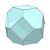W8 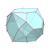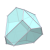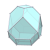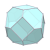W9 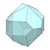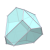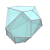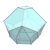W10 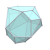Features of Waterman Polyhedra So the nice thing is, the creation of the polyhedra is done parametrically, in other words, systematically. Needless to say, there are infinite of Waterman polyhedra, and interestingly there are doubles to be encountered, where: the same amount of packed spheres result in the same polyhedra (14 + 16 n) m2 (whereas n & m integers >= 0) the final polyhedra from packed spheres result in a previous discovered polyhedra when normalized (e.g. W3 O1 = W24 O1) Those are not yet removed in the overview which follows. Platonic & Archimedean Solids vs Waterman Polyhedra The Waterman Polyhedra (WP) covers also some of the platonic and archimedean solids. For sake of this comparison the WP are normalized, as W2 O1 has a different size/volume than W1 O6, but the same form of a Octahedron. Platonic Solids Waterman W1 O4 Waterman W2 O1 Waterman W2 O6 W1 O3* = W2 O3* = W1 O3 = W1 O4 = Tretrahedron W2 O1 = W1 O6 = Octahedron W2 O6 = Cube Icosahedron and Dodecahedron have no WP representation. Archimedean Solids Waterman W1 O1 Waterman W10 O1 Waterman W2 O4 W1 O1 = W4 O1 = Cuboctahedron W10 O1 = Truncated Octahedron W4 O3 = W2 O4 = Truncated Tetrahedron The following look like archimedean solids, but they are not: Waterman W7 O1 Waterman W3 O1 W7 O1 != Truncated Cuboctahedron W3 O1 = W12 O1 != Rhombicuboctahedron as they are not having one length of edge, but two lengths of edges. The others have no WP representation. The Generalized Waterman Polyhedra (GWP) are currently still sorted by Steve Waterman, and I will include them later as they may cover more platonic and archimedean solids. References Waterman Polyhedron , very informative site by Steve Waterman, the inventor of the Waterman polyhedra Paul Bourke has also a comprehensive website (I highly recommend to visit), his waterman.c I used to calculate those rendered Waterman polyhedra. 3D Junkyard , vast & interesting collection of links by David Eppstein (End of Article) Page << Prev | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Next >> Content: Page 1: Introduction, Platonic Solids, Archimedean Solids, Tetrahedron, Truncated Tetrahedron, Octahedron ... Page 2: Johnson Solids Page 3: Square Pyramid, Historic Pyramids, Pentagonal Pyramid, Triangular Cupola, Square Cupola, Pentagonal Cupola ... Page 4: Gyroelongated Pentagonal Rotunda, Gyrobifastigium, Triangular Orthobicupola, Square Orthobicupola ... Page 5: Augmented Triangular Prism, Biaugmented Triangular Prism, Triaugmented Triangular Prism ... Page 6: Parabigyrate Rhombicosidodecahedron, Metabigyrate Rhombicosidodecahedron, Trigyrate Rhombicosidodecahedron ... Page 7: Uniform Polyhedra, References Page 8: Waterman Polyhedra, Some More Examples, Different Origins, Features of Waterman Polyhedra ... Home   ·   About   ·   Tipi   ·   Yurt   ·   Dome   ·   Features   ·   Gallery Print   ·   Bookmark Creative Commons (CC) BY-SA-NC 2005-2017, developed, designed and written by René K. Müller Graphics & illustrations made with Inkscape, Tgif, Gimp, PovRay, GD.pm Web-Site powered by FreeBSD & Debian/Linux - 100% Open Source