UpdatesSun, November 22, 2009: Rudimentary information, needs more math and background research
.
|
also known as
Polyhedral Zome or
Crystal Zome

 Zome Building (n=12) |
The term "
Zome 
" comes from "
zonohedron 
" + "
dome", and was coined sometime in 1970 by Steve Durkee.
A zonohedron is a form which can fill a given space seamless, the most popular zonohedron is the cube.
Strictly speaking, the zomes featured here aren't zonohedra anymore; it seems the term "zome" also applies to unusual dome constructions.
While I was looking for some clarification of the term "Zome", I include three significant ones I came across:
Rob Bell  writes in an email to me:
writes in an email to me:
The term Zome is overloaded and the exact meaning does depend on the context - ie; does one mean the toy? For me a zome is any structure which utilizes zonohedral geometry for a real world structure - a shelter of some sort. And more specifically a zome is such a shelter based upon a class of zonohedra known as polar zonohedra. Mathematically speaking, polar zonohedra are 3 dimensional projections of higher dimensional cubes.
whereas Mathworld.com  further defines:
further defines:
A polar zonohedron is a convex zonohedron derived from the star which joins opposite vertices of any right n-gonal prism (for n even) or antiprism (for n odd). The faces of this zonohedron consist of n equal rhombs surrounding one vertex, n rhombs beyond these, and so on, giving n-1 sets of n rhombs altogether that end with those surrounding the opposite vertex.
(Franklin 1937; Coxeter 1973, p. 29)
As n -> infinite, the polar zonohedron of order n approaches a solid of revolution created by rotation of a sine curve (Chilton and Coxeter 1963, Towle 1996).
And further, a quote from Russel Towle in the Whole Earth Catalog:
Zome is a word coined by Steve Baer as I recall, based upon "dome", the difference being that the geodesic dome of Buckminster Fuller was formed upon a network of triangles, wheres zomes are bounded by zonogons, a zonogon being a convex, centrally-symmetrical polygon. A rhomb is a zonogon, so are all regular polygons with an even number of sides, but a zonogon need not be regular.
Florian Tuczek  writes on his web-site:
writes on his web-site:
A zome has structural similarities to the quasicrystals discovered not before the nineteen-eighties. Quasicrystals do not have a solid global grid like crystals, but merely local symmetries. A zome is formed of zonohedra or fragments of them. Zonohedra are convex polyhedra of lozenge-shaped faces.
Zonohedra and Zomes are characterised by groups of lozenges with parallel edges forming zones, which can be removed or added to make the structure grow or shrink. The irregularity and their partial symmetries produce mental associations to structures in living nature - in contrast to the "real" crystals.
On the borders of a zonohedral shell structure, the lozenge-shaped faces can be cut in half or in quarters in order to get on these cuts flat oblong horizontal faces lying upon a ground plane - or flat oblong vertical faces adjacent to a vertical wall. Furthermore, Zomes can be extended or changed by additional faces having other shapes than a lozenge.
Yann Lipnick  on the other hand writes on his web-site:
on the other hand writes on his web-site:
Zomes are geometric volumes composed of lozenges arranged in a double spiral. This family of shapes, of which one find traces in sacred architecture, has a relationship with the laws that govern the living world.
We find these shapes in numerous natural forms such as crystals, honeycombs, and certain plants (pineapples, pine cones, artichokes, etc...).
So, the term "zome" is a rather generic term for lozenge based structures, yet, mathematically speaking the term covers a much vaster amount of forms.

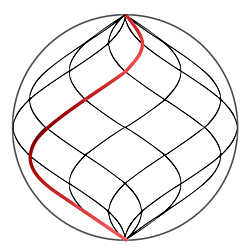
 Polyhedral Helix Zome (n=12) |
In order to create a polyhedral structure, the helix zome cone is split in half, to create a dome-like structure. Further, the half helix is truncated into
n-steps.
One of the obvious advantages is that the struts are all
the same length, yet, the area they cover changes - all are rhombuses.
The most prominant disadvantages are that there is no native triangulation, therefore the structure is instable.
If you insist on triangulation, a necessity for a real life application, you end up with n strut lengths, and n-1 different faces.
Further, the pointy top of the zome is ideal for snow slide and general avoiding rainwater or snow on the top of the habitat, and is a slight advantage over the pure hemispherical dome approach.
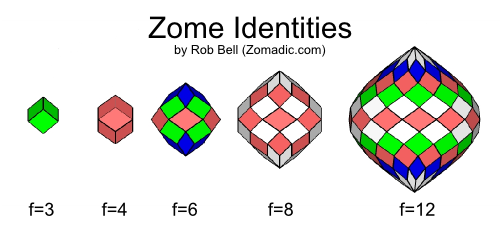
Rob Bell pointed out to me, that facets of lower frequencies can be reused for larger frequencies as his illustration shows; yet, the larger frequency also a larger diameter is required.
Follows later ...

Zome 12
2001/12/02 14:05

Zome 12 - Interior
2001/12/02 14:22

Zome 12 - Construction 1
2001/03/30 12:59

Zome 12 - Construction 2
2000/01/23 16:27

Zome 12 - Construction 3
1999/06/08 10:31

Zome 12 - Construction 4
2009/12/01 10:11

Zome Tents
2000/12/09 23:34
As you can notice, in the real world application the rhombuses are triangulated.
Zomadic.com 
has some artistic approaches to the zome theme:
.jpg)
Zomadic - Sunrise through the Zome (Burning Man 2009)
2009/11/22 14:06
 3.jpg)
Zomadic - In the Desert (Burning Man 2009) 3
2009/11/22 14:05
.jpg)
Zomadic - See through (Burning Man 2009)
2009/11/22 14:05
.jpg)
Zomadic - See through 2 (Burning Man 2009)
2009/11/22 14:06

Zomicil 1
2009/11/24 16:39

Zomicil 3
2009/11/24 16:38

Zomicil - Interior 1
2009/11/24 16:37

Zomicil - Construction
2009/11/24 16:38
As a side note, Rob produced the parts of the zomes using a CNC machine to cut the pieces - a digital production.
A "skinned" version of his zomes, a green house:

Algarden Zome
2009/11/24 16:40

Algarden Zome
2009/11/24 16:41

Algarden Zome Construction 1
2009/11/24 16:42

Algarden Zome Construction 2
2009/11/24 16:45

Algarden Zome Ornament Detail
2009/11/24 16:41

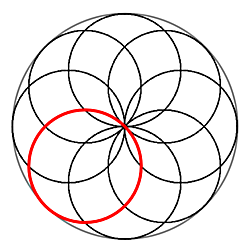
 Helix Zome |
Interestingly, a curved version was developed by Nicolas Causse starting with the polyhedral form first and then smoothed it - I feature his approach at
Helix Zome.
.:.

 " comes from "zonohedron
" comes from "zonohedron  " + "dome", and was coined sometime in 1970 by Steve Durkee.
A zonohedron is a form which can fill a given space seamless, the most popular zonohedron is the cube.
" + "dome", and was coined sometime in 1970 by Steve Durkee.
A zonohedron is a form which can fill a given space seamless, the most popular zonohedron is the cube.
 has some artistic approaches to the zome theme:
has some artistic approaches to the zome theme:














.jpg)
 3.jpg)
.jpg)
.jpg)











