Introduction
After a some research I composed following comprehensive overview:
- 5 Platonic Solids, regular faces: triangle, square or pentagon only
- 13 Archimedean Solids, semi-regular faces: triangle, square and pentagon
- 92 Johnson Solids, semi-regular faces: triangle, square, penta-, hexa-, octa- and decagons
- 80 Uniform Polyhedra, incl. platonic & archimedean solid and many concave forms not suitable for habitats
- Waterman Polyhedra, parametrically created, which include also some platonic and archimedean solids
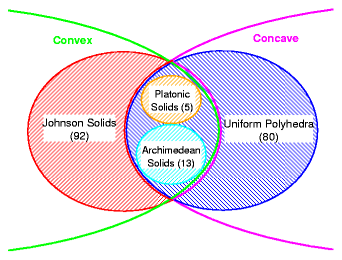 |
So a total of 110 convex and 62 concave polyhedra plus apprx. 500 convex parametrical created Waterman polyhedra are listed on the next pages of this document.
A hint on name convention:
|
|
|
|
thereby polygons ('gon' from greek 'gonu' (knee or angle)) of n-sides:
|
|
|
Based on the study here of suitable solids or polyhedra I extract geodesic variants and from there I sort out those finally which are suitable for dome construction.
Note: The page structure might change depending how much info I will include in the future, e.g. multiple pages or separate pages for each form. Let's see.
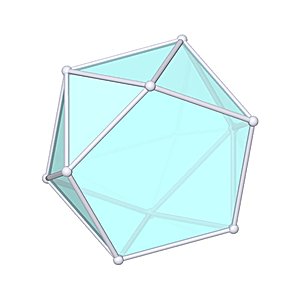
Platonic Solids
 Tetrahedron |  Octahedron |  Cube |  Icosahedron |
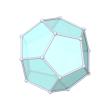 Dodecahedron |
  Neolithic Carved Stones |
 , but those forms have been discovered in Scotland and are dated 2000-3200 BC and relate to the "neolithic" or "new stone age" people of that time (see also George Hart: Neolithic Carved Stone Polyhedra
, but those forms have been discovered in Scotland and are dated 2000-3200 BC and relate to the "neolithic" or "new stone age" people of that time (see also George Hart: Neolithic Carved Stone Polyhedra  ).
For more infos see Google: Carved Stone Balls
).
For more infos see Google: Carved Stone Balls  .
.
Archimedean Solids
The base information is compiled from Wikipedia  and Mathworld
and Mathworld  and "Uniform solution for uniform polyhedra" by Zvi Har'El
and "Uniform solution for uniform polyhedra" by Zvi Har'El  , merged all that information and additionally listed V, A, and rinner and router with a calculator.
I also plan to comment on each form, and suggest usage for a temporary building, especially if further triangulation like with the icosahedron to geodesic domes.
, merged all that information and additionally listed V, A, and rinner and router with a calculator.
I also plan to comment on each form, and suggest usage for a temporary building, especially if further triangulation like with the icosahedron to geodesic domes.
Symbols:
- s = strut length
- V = volume
- A = surface area
- rinner = inner radius or inradius
- router = outer radius or circumradius
- ravg = (rinner + router) / 2
Duals of a solid is when the solids' vertices become faces and vice-versa.
Edit the fields with yellow background and hit ENTER or TAB to (re)calculate the other values.
Note: I still need to cross-check all expressions (V, A, rinner and router) by other sources, so don't rely on it yet.
Tetrahedron
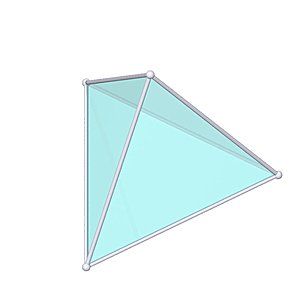  Tetrahedron |
- Uniform Polyhedron: U1
- Platonic Solid
- Platonic Element: Fire
- Vertices: 4
- Edges: 6
- Faces: 4
- Wythoff symbol: 3|2 3
- Symmetry Group: {3, 3, 3}
- Vertex Configuration: tetrahedral
- Dual: tetrahedron
- V: s3 / 12 * √2
- A: s2 * √3
- rinner: s / 12 * √6
- router: s / 4 * √6
- h: s / 3 * √6
Truncated Tetrahedron
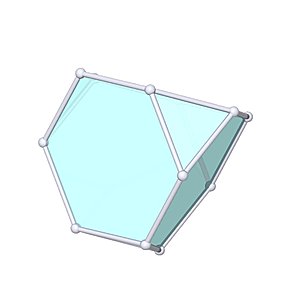  Truncated Tetrahedron |
- Uniform Polyhedron: U2
- Archimedean Solid: A13
- Vertices: 12
- Edges: 18
- Faces: 8
- Wythoff symbol: 2 3|3
- Symmetry Group: tetrahedral
- Vertex Configuration: {6, 6, 3}
- Dual: triakis tetrahedron
- V: s3 * 23/12 * √2
- A: s2 * 7 * √3
- rinner: s * 9 / 44 * √22
- router: s / 4 * √22

Octahedron
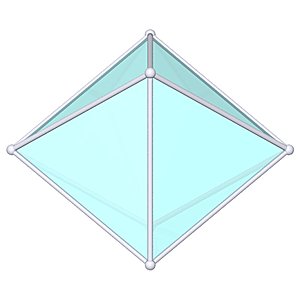  Octahedron |
- Uniform Polyhedron: U5
- Platonic Solid
- Platonic Element: Air
- Vertices: 6
- Edges: 12
- Faces: 8
- Wythoff symbol: 4|2 3
- Symmetry Group: octahedral
- Vertex Configuration: {3, 3, 3, 3}
- Dual: cube
- V: s3 / 3 * √2
- A: s2 * 8 / 4 * √3
- rinner: s / 6 * √6
- router: s / 2 * √2
Half of an octahedron is the classic pyramid.
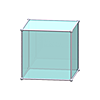
Cube
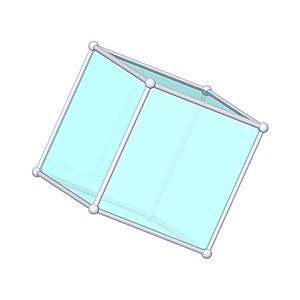  Cube |
- Uniform Polyhedron: U6
- aka Hexahedron
- Platonic Solid
- Platonic Element: Earth
- Vertices: 8
- Edges: 12
- Faces: 6
- Wythoff symbol: 3|2 4
- Symmetry Group: octahedral
- Vertex Configuration: {4, 4, 4}
- Dual: octahedron
- V: s3
- A: s2 * 6
- rinner: s / 2
- router: s / 2 * √3

It's one of the main forms of western architecture, and one of the main zonohedra (aka parallelohedron), the ability to tile space without holes. There are many more possible, more complex with more faces.
- Zonohedron
 , Wikipedia
, Wikipedia
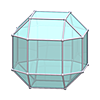
Cuboctahedron
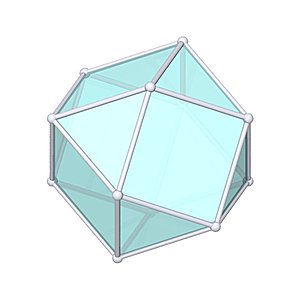  Cuboctahedron |
- Uniform Polyhedron: U7
- Archimedean Solid: A1
- Vertices: 12
- Edges: 24
- Faces: 14
- Wythoff symbol: 2|3 4
- Symmetry Group: octahedral
- Vertex Configuration: {3, 4, 3, 4}
- Dual: rhombic dodecahedron
- V: s3 * 5/3 * √2
- A: s2 * (6 + 2 * √3)
- rinner: s * 3/4
- router: s
Truncated Octahedron
  Truncated Octahedron |
- Uniform Polyhedron: U8
- Archimedean Solid: A12
- Vertices: 24
- Edges: 36
- Faces: 14
- Wythoff symbol: 2 4|3
- Symmetry Group: octahedral
- Vertex Configuration: {6, 6, 4}
- Dual: tetrakis hexahedron
- V: s3 * 8 * √2
- A: s2 * (6 + 12 * √3)
- rinner: s * 9/20 * √10
- router: s / 2 * √10
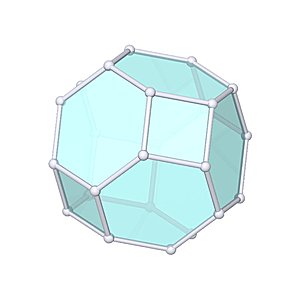
Truncated Cube
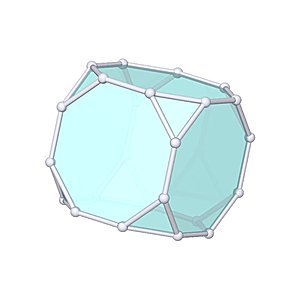  Truncated Cube |
- Uniform Polyhedron: U9
- Archimedean Solid: A9
- Vertices: 24
- Edges: 36
- Faces: 14
- Wythoff symbol: 2 3|4
- Symmetry Group: octahedral
- Vertex Configuration: {8, 8, 3}
- Dual: triakis octahedron
- V: s3 / 3 * (21 + 14 * √2)
- A: s2 * 2 * (6 + 6 * √2 + √3)
- rinner: s / 17 * (5 + 2 * √2 * √(7 + 4 * √2))
- router: s / 2 * √(7 + 4 * √2)
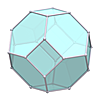
Rhombicuboctahedron
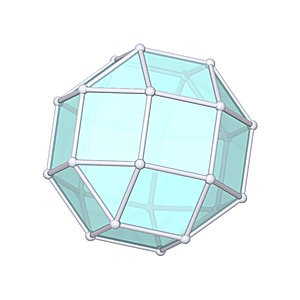  Rhombicuboctahedron |
- Uniform Polyhedron: U10
- aka Small Rhombicuboctahedron
- Archimedean Solid: A6
- Vertices: 24
- Edges: 48
- Faces: 26
- Wythoff symbol: 3 4|2
- Symmetry Group: octahedral
- Vertex Configuration: {4, 3, 4, 4}
- Dual: deltoidal icositetrahedron
- V: s3 / 3 * (12 + 10 * √2)
- A: s2 * (18 + 2 * √3)
- rinner: s / 17 * (6 + √2) * √(5 + 2 * √2)
- router: s / 2 * √(5 + 2 * √2)
Truncated Cuboctahedron
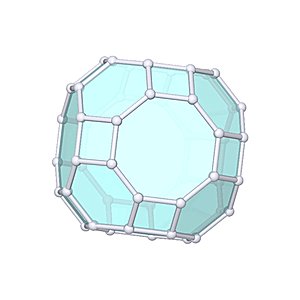  Truncated Cuboctahedron |
- Uniform Polyhedron: U11
- aka Great Rhombicuboctahedron
- Archimedean Solid: A3
- Vertices: 48
- Edges: 72
- Faces: 26
- Wythoff symbol: 2 3 4|
- Symmetry Group: octahedral
- Vertex Configuration: {4, 6, 8}
- Dual: disdyakis dodecahedron
- V: s3 * (22 + 14 * √2)
- A: s2 * 12 * (2 + √2 + √3)
- rinner: s * 3/97 * (14 + √2) * √(13 + 6 * √2)
- router: s / 2 * √(13 + 6 * √2)
Snub Cube
  Snub Cube |
- Uniform Polyhedron: U12
- aka Cubus Simus
- aka Snub Cuboctahedron
- Archimedean Solid: A7
- Vertices: 24
- Edges: 60
- Faces: 38
- Wythoff symbol: |2 3 4
- Symmetry Group: octahedral
- Vertex Configuration: {3, 3, 3, 3, 4}
- Dual: pentagonal icositetrahedron
- t: 1/3 * (1 + (10-3*√33)(1/3) + (19+3*√33)(1/3) )
- V: s3 * ( 8/3 * √(3 * (3-t)/(4*(2-t)) - 1) + √(4 * (3-t)/(4*(2-t)) -2) )
- V: s3 * √((613 * t + 203)/(9*(35*t-62)))
- A: s2 * (6 + 8 * √3)
- rinner: s * √(abs(1-t)/(4*(2-t)))
- router: s * √((3-t)/(4*(2-t)))
Icosahedron
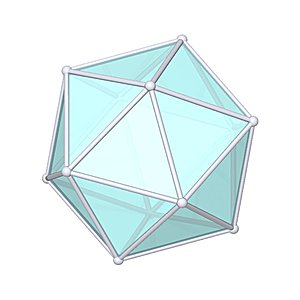  Icosahedron |
- Uniform Polyhedron: U22
- Platonic Solid
- Platonic Element: Water
- Vertices: 12
- Edges: 30
- Faces: 20
- Wythoff symbol: 5|2 3
- Symmetry Group: icosahedral
- Vertex Configuration: {3, 3, 3, 3, 3}
- Dual: dodecahedron
- V: s3 * 5/12 * (3 + √5)
- A: s2 * 20 / 4 * √3
- rinner: s / 12 * (3 * √3 + √15)
- router: s / 4 * √(10 + 2 * √5)
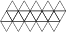
One variant of a geodesic dome can be derived from the Icosahedron.
Dodecahedron
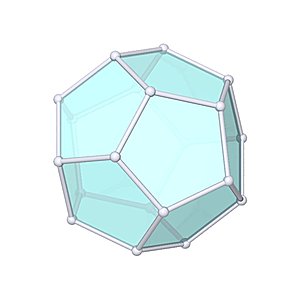  Dodecahedron |
- Uniform Polyhedron: U23
- Platonic Solid
- Platonic Element: Ether
- Vertices: 20
- Edges: 30
- Faces: 12
- Wythoff symbol: 3|2 5
- Symmetry Group: icosahedral
- Vertex Configuration: {5, 5, 5}
- Dual: icosahedron
- V: s3 / 4 * (15 + 7 * √5)
- A: s2 * 12 / 4 * √(25 + 10 * √5)
- rinner: s / 20 * √(250 + 110 * √5)
- router: s / 4 * (√15 + √3)
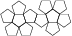
Icosidodecahedron
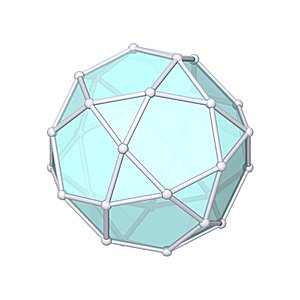  Icosidodecahedron |
- Uniform Polyhedron: U24
- Archimedean Solid: A4
- Vertices: 30
- Edges: 60
- Faces: 32
- Wythoff symbol: 2|3 5
- Symmetry Group: icosahedral
- Vertex Configuration: {3, 5, 3, 5}
- Dual: rhombic triacontahedron
- V: s3 / 6 * (45 + 17 * √5)
- A: s2 * (5 * √3 + 3 * √5 * √(5 + 2 * √5))
- rinner: s / 8 * (5 + 3 * √5)
- router: s * (1 + √5) / 2
Truncated Icosahedron
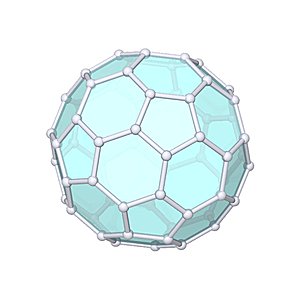  Truncated Icosahedron |
- Uniform Polyhedron: U25
- Archimedean Solid: A11
- Vertices: 60
- Edges: 90
- Faces: 32
- Wythoff symbol: 2 5|3
- Symmetry Group: icosahedral
- Vertex Configuration: {6, 6, 5}
- Dual: pentakis dodecahedron
- V: s3 / 4 * (125 + 43 * √5)
- A: s2 * 3 * (10 * √3 + √5 * √(5 + 2 * √5))
- rinner: s * 9/872 * (21 + √5) * √(58 + 18 * √5)
- router: s / 4 * √(58 + 18 * √5)
Truncated Dodecahedron
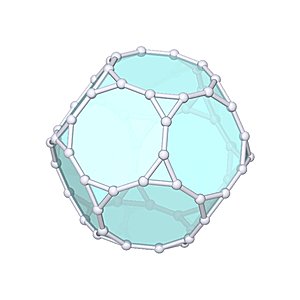  Truncated Dodecahedron |
- Uniform Polyhedron: U26
- Archimedean Solid: A10
- Vertices: 60
- Edges: 90
- Faces: 32
- Wythoff symbol: 2 3|5
- Symmetry Group: icosahedral
- Vertex Configuration: {10, 10, 3}
- Dual: triakis icosahedron
- V: s3 * 5/12 * (99 + 47 * √5)
- A: s2 * 5 * (√3 + 6 * √(5 + 2 * √5))
- rinner: s * 5/488 * (17 * √2 + 3 * √10) * √(37 + 15 * √5)
- router: s / 4 * √(74 + 30 * √5)
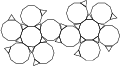
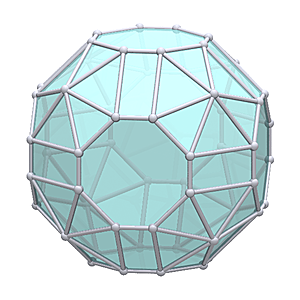
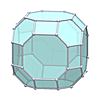
Rhombicosidodecahedron
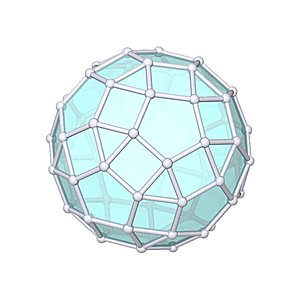  Rhombicosidodecahedron |
- Uniform Polyhedron: U27
- aka Small Rhombicosidodecahedron
- Archimedean Solid: A5
- Vertices: 60
- Edges: 120
- Faces: 62
- Wythoff symbol: 3 5|2
- Symmetry Group: icosahedral
- Vertex Configuration: {4, 3, 4, 5}
- Dual: deltoidal hexecontahedron
- V: s3 / 3 * (60 + 29 * √5)
- A: s2 * (30 + √(30 * (10 + 3 * √5 + √(15 * (5 + 2 * √5)))))
- rinner: s / 41 * (15 + 2 *√5) * √(11 + 4 * √5)
- router: s / 2 * √(11 + 4 * √5)
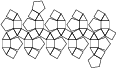
Truncated Icosidodecahedron
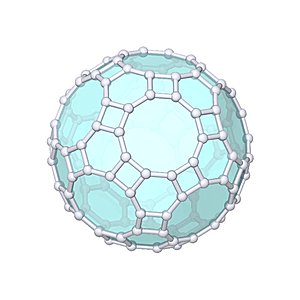  Truncated Icosidodecahedron |
- Uniform Polyhedron: U28
- aka Great Rhombicosidodecahedron (which actually is misleading as it also references U67 "(Uniform) Great Rhombicosidodecahedron")
- aka Rhombitruncated Icosidodecahedron
- aka Omnitruncated Icosidodecahedron
- Archimedean Solid: A2
- Vertices: 120
- Edges: 180
- Faces: 62
- Wythoff symbol: 2 3 5|
- Symmetry Group: icosahedral
- Vertex Configuration: {4, 6, 10}
- Dual: disdyakis triacontahedron
- V: s3 * (95 + 50 * √5)
- A: s2 * 30 * (1 + √(2 * (4 + √5 + √(15 + 6 * √6))))
- rinner: s * 1/241 * (105 + 6 * √5 * √(31 + 12 * √5))
- router: s / 2 * √(31 + 12 * √5)
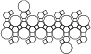
Snub Dodecahedron
  Snub Dodecahedron |
- Uniform Polyhedron: U29
- Archimedean Solid: A8
- Vertices: 60
- Edges: 150
- Faces: 92
- Wythoff symbol: |2 3 5
- Symmetry Group: icosahedral
- Vertex Configuration: {3, 3, 3, 3, 5}
- Dual: pentagonal hexecontahedron
- V: s3 * 3.7543
- A: s2 * √(15 * (95 + 6 * √5 + 8 * √(15 * (5 + 2 * √5))))
- rinner: s * 2.03987315
- router: s * 2.15583737
(Note: the volume for this solid is only available numerically, not symbolical - if you can provide me with the expression for V let me know).
References
- Platonic Solid
 , Wikipedia
, Wikipedia
- Platonic Solid
 , Mathworld
, Mathworld
- Archimedean Solid
 , Wikipedia
, Wikipedia
- Archimedean Solid
 , Mathworld
, Mathworld
- Platonic & Archimedean Solid Paper Models

- Zonohedron
 , convex polyhedron tiling space without "holes", Wikipedia
, convex polyhedron tiling space without "holes", Wikipedia
- Deltahedron
 , Mathworld
, Mathworld
- Zvi Har'El's Homepage
 , author of Uniform Solution for Uniform Polyhedra
, author of Uniform Solution for Uniform Polyhedra  and kaleido
and kaleido 
- Uniform Polyhedra
 by Paul Bourke
by Paul Bourke
- Uniform Polyhedra
 povray files prepared by Russel Towle, which I used to render the models
povray files prepared by Russel Towle, which I used to render the models
- Woven Paper Polyhedra
 , using woven paper to construct polyhedra
, using woven paper to construct polyhedra
Johnson Solids
In 1966 Norman Johnson published a paper
"Convex Solids with Regular Faces" (Canadian Journal of Mathematics, Vol. 18, 1966, pp. 169-200)
in which he classified and named 92 types of convex polyhedra which are composed by same side length additionally to the platonic and archimedean solids:
published a paper
"Convex Solids with Regular Faces" (Canadian Journal of Mathematics, Vol. 18, 1966, pp. 169-200)
in which he classified and named 92 types of convex polyhedra which are composed by same side length additionally to the platonic and archimedean solids:
As the time goes by I will comment those forms which look promising for a temporary building.
Square Pyramid
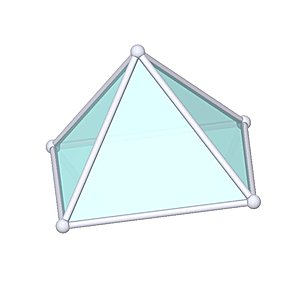  Square Pyramid |
- Johnson Solid: J1
- Vertices: 5
- Faces: 5
- Edges: 8
- V: s3 / 6 * √2
- A: s2 * (1 + √3)
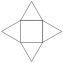
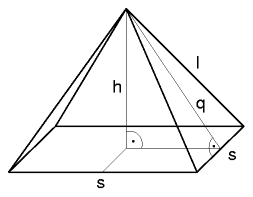 General Pyramid |
- q = √((s/2)2 + h2)
- l = √((s/2)2 + q2)
- A = 2 s q + s2
- Awall/roof = 2 s q
- V = s2 h / 3
Historic Pyramids
  The Pyramids of Giza (courtesy Bruno Girin/DHD Multimedia Gallery  ) ) |
The largest pyramid in Giza is the Khufu Pyramid, with following values:
- s = 231m (original) (now: 230.4m)
- h = 146.6m (original) (now: 138.8m)
thereby
- q = 186.632m
- l = 219.478m
Interesting ratio:
- s/h = 1.57571.. ~ π/2 ~ 11/7
Read more at Great Pyramid of Giza  .
.
Pentagonal Pyramid
  Pentagonal Pyramid |
- Johnson Solid: J2
- Vertices: 6
- Faces: 6
- Edges: 10
- V: s3 / 24 * (5 + √5)
- A: s2 / 2 * √(5/2 * (10 + √10 + √(75+30*√5))
The roof isn't very steep, unless those roof struts would be made longer - it would be a very simplistic habitat.
Triangular Cupola
  Triangular Cupola |
- Johnson Solid: J3
- Vertices: 9
- Faces: 8
- Edges: 15
- V: s3 * (5/(5*√2))
- A: s2 * (3+5/2*√3)
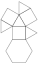
Square Cupola
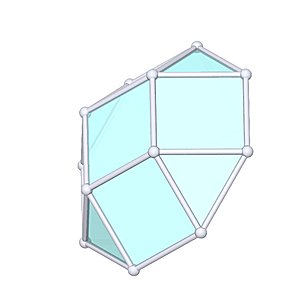  Square Cupola |
- Johnson Solid: J4
- Vertices: 12
- Faces: 10
- Edges: 20
Also cap of a Rhombicuboctahedron.
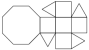
Pentagonal Cupola
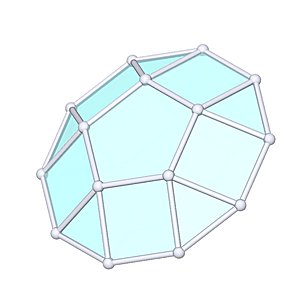  Pentagonal Cupola |
- Johnson Solid: J5
- Vertices: 15
- Faces: 12
- Edges: 25
- V: s3 / 6 * (5+4*√5)
- A: s2 / 4 * (20+√(10*(80+31*√5+√(2175+950*√5))))
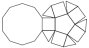
Also cap of a Rhombicosidodecahedron.
Pentagonal Rotunda
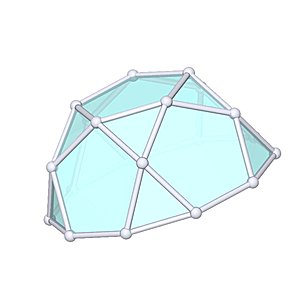  Pentagonal Rotunda |
- Johnson Solid: J6
- Vertices: 20
- Faces: 17
- Edges: 35
- V: s3 / 12 * (45+17*√5)
- A: s2 * 5/2 * (√3+√(26+(58/√5)))
- h: s * √(1/5*(5+2*√5))
Elongated Triangular Pyramid
  Elongated Triangular Pyramid |
- Johnson Solid: J7
- Vertices: 7
- Faces: 7
- Edges: 12
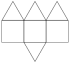
Elongated Square Pyramid
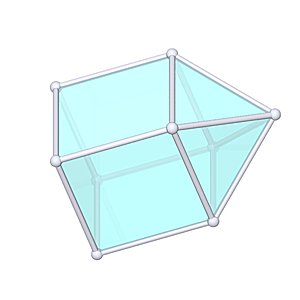  Elongated Square Pyramid |
- Johnson Solid: J8
- Vertices: 9
- Faces: 9
- Edges: 16
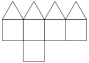
Elongated Pentagonal Pyramid
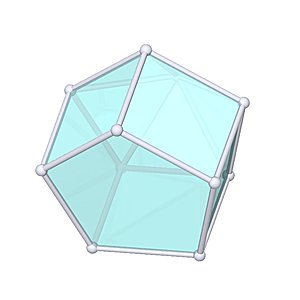  Elongated Pentagonal Pyramid |
- Johnson Solid: J9
- Vertices: 11
- Faces: 11
- Edges: 20
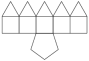
Gyroelongated Square Pyramid
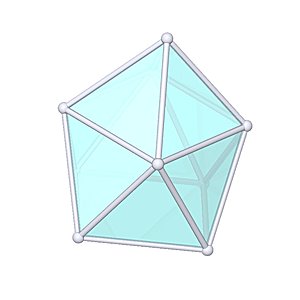  Gyroelongated Square Pyramid |
- Johnson Solid: J10
- Vertices: 9
- Faces: 13
- Edges: 20
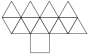
Gyroelongated Pentagonal Pyramid
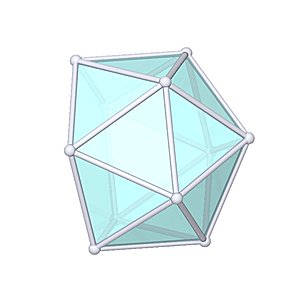  Gyroelongated Pentagonal Pyramid |
- Johnson Solid: J11
- Vertices: 11
- Faces: 16
- Edges: 25
Triangular Dipyramid
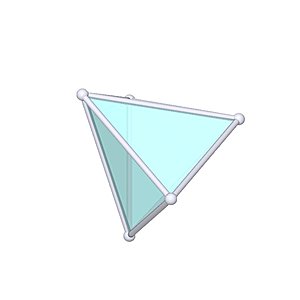  Triangular Dipyramid |
- Johnson Solid: J12
- Vertices: 5
- Faces: 6
- Edges: 9
Pentagonal Dipyramid
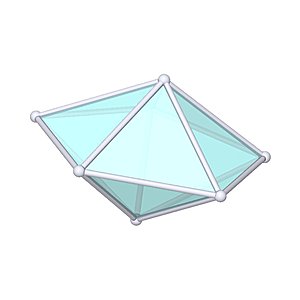  Pentagonal Dipyramid |
- Johnson Solid: J13
- Vertices: 7
- Faces: 10
- Edges: 15
- V: s3 / 12 * (5 + √5)
- A: s2 * 5/12 * √3
- router: s / 10 * √(50+10*√5)
- h: s / 10 * √(50-10*√5)

Elongated Triangular Dipyramid
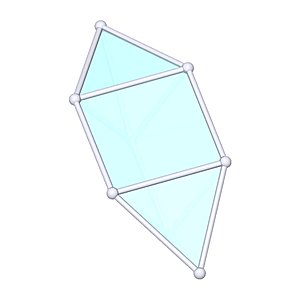  Elongated Triangular Dipyramid |
- Johnson Solid: J14
- Vertices: 8
- Faces: 9
- Edges: 15
Elongated Square Dipyramid
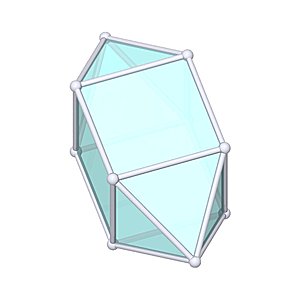  Elongated Square Dipyramid |
- Johnson Solid: J15
- Vertices: 10
- Faces: 12
- Edges: 20
Elongated Pentagonal Dipyramid
  Elongated Pentagonal Dipyramid |
- Johnson Solid: J16
- Vertices: 12
- Faces: 15
- Edges: 25
Gyroelongated Square Dipyramid
  Gyroelongated Square Dipyramid |
- Johnson Solid: J17
- Vertices: 10
- Faces: 16
- Edges: 24
- V: s3 * 2(1/4) / 4 * (1 + √2 + 2(1/4) )
- A: s2 * 4 * √3
Elongated Triangular Cupola
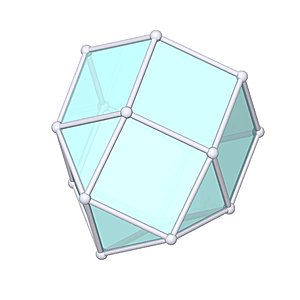  Elongated Triangular Cupola |
- Johnson Solid: J18
- Vertices: 15
- Faces: 14
- Edges: 27
Elongated Square Cupola
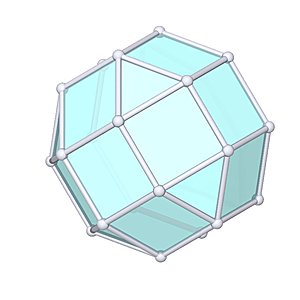  Elongated Square Cupola |
- Johnson Solid: J19
- Vertices: 20
- Faces: 18
- Edges: 36

Elongated Pentagonal Cupola
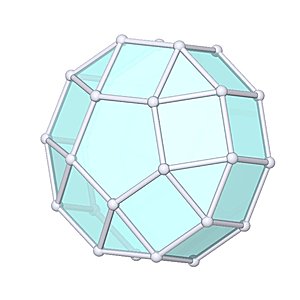  Elongated Pentagonal Cupola |
- Johnson Solid: J20
- Vertices: 25
- Faces: 22
- Edges: 45
Elongated Pentagonal Rotunda
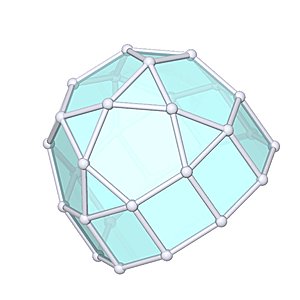  Elongated Pentagonal Rotunda |
- Johnson Solid: J21
- Vertices: 30
- Faces: 27
- Edges: 55
Gyroelongated Triangular Cupola
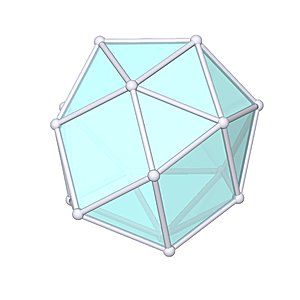  Gyroelongated Triangular Cupola |
- Johnson Solid: J22
- Vertices: 15
- Faces: 20
- Edges: 33
Gyroelongated Square Cupola
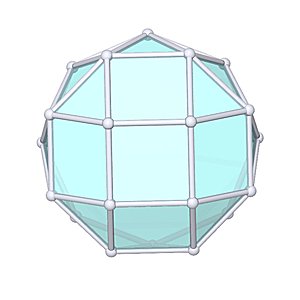  Gyroelongated Square Cupola |
- Johnson Solid: J23
- Vertices: 20
- Faces: 26
- Edges: 44
Gyroelongated Pentagonal Cupola
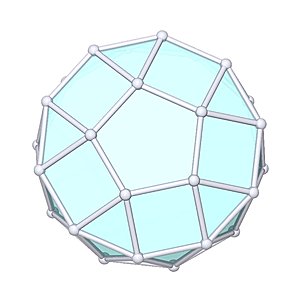  Gyroelongated Pentagonal Cupola |
- Johnson Solid: J24
- Vertices: 25
- Faces: 32
- Edges: 55
Gyroelongated Pentagonal Rotunda
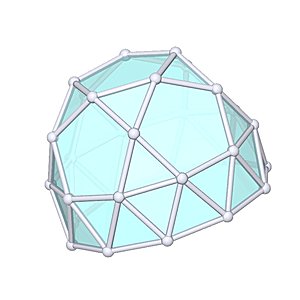  Gyroelongated Pentagonal Rotunda |
- Johnson Solid: J25
- Vertices: 30
- Faces: 37
- Edges: 65
Gyrobifastigium
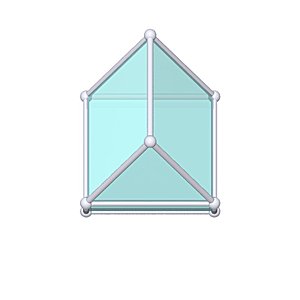  Gyrobifastigium |
- Johnson Solid: J26
- Vertices: 8
- Faces: 8
- Edges: 14
Triangular Orthobicupola
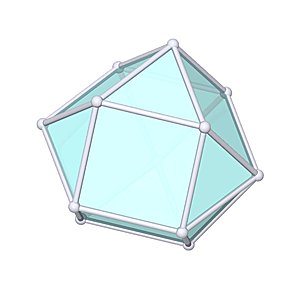  Triangular Orthobicupola |
- Johnson Solid: J27
- Vertices: 12
- Faces: 14
- Edges: 24
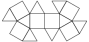
Square Orthobicupola
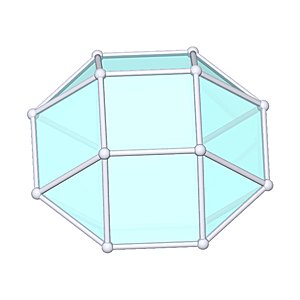  Square Orthobicupola |
- Johnson Solid: J28
- Vertices: 16
- Faces: 18
- Edges: 32
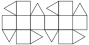
Square Gyrobicupola
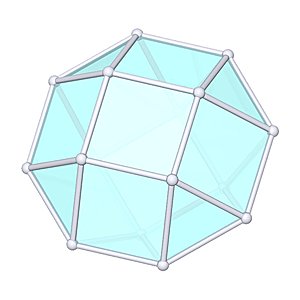  Square Gyrobicupola |
- Johnson Solid: J29
- Vertices: 16
- Faces: 18
- Edges: 32
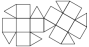
Pentagonal Orthobicupola
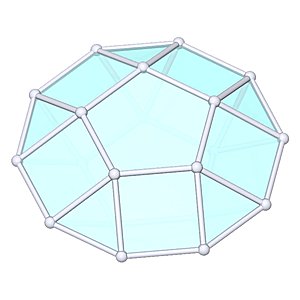  Pentagonal Orthobicupola |
- Johnson Solid: J30
- Vertices: 20
- Faces: 22
- Edges: 40
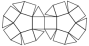
Pentagonal Gyrobicupola
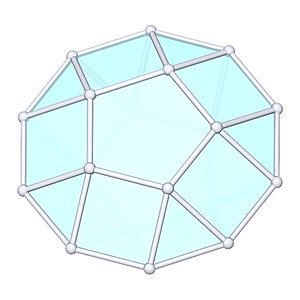  Pentagonal Gyrobicupola |
- Johnson Solid: J31
- Vertices: 20
- Faces: 22
- Edges: 40
Pentagonal Orthocupolarontunda
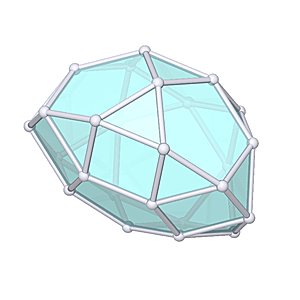  Pentagonal Orthocupolarontunda |
- Johnson Solid: J32
- Vertices: 25
- Faces: 27
- Edges: 50
Pentagonal Gyrocupolarotunda
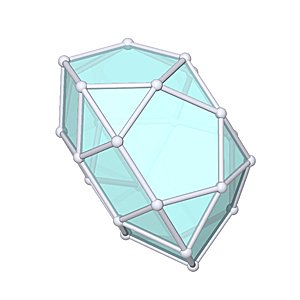  Pentagonal Gyrocupolarotunda |
- Johnson Solid: J33
- Vertices: 25
- Faces: 27
- Edges: 50
Pentagonal Orthobirotunda
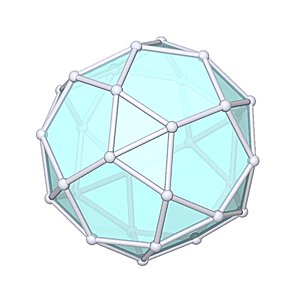  Pentagonal Orthobirotunda |
- Johnson Solid: J34
- Vertices: 30
- Faces: 32
- Edges: 60
Elongated Triangular Orthobicupola
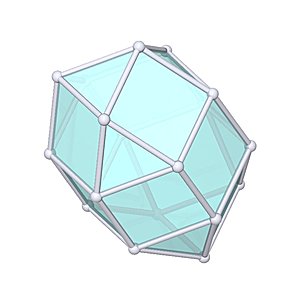  Elongated Triangular Orthobicupola |
- Johnson Solid: J35
- Vertices: 18
- Faces: 20
- Edges: 36
Elongated Triangular Gyrobicupola
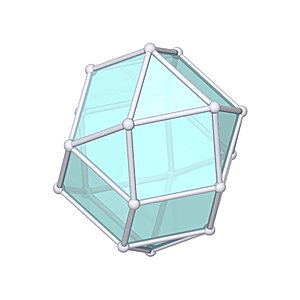  Elongated Triangular Gyrobicupola |
- Johnson Solid: J36
- Vertices: 18
- Faces: 20
- Edges: 36
Elongated Square Gyrobicupola
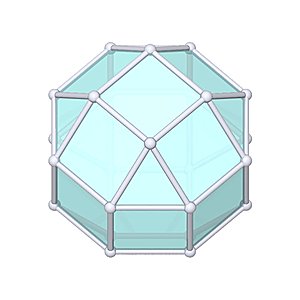  Elongated Square Gyrobicupola |
- Johnson Solid: J37
- Vertices: 24
- Faces: 26
- Edges: 48
Elongated Pentagonal Orthobicupola
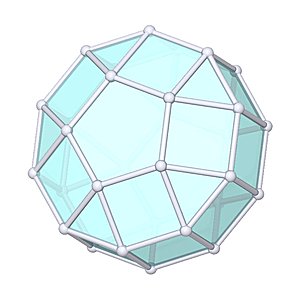  Elongated Pentagonal Orthobicupola |
- Johnson Solid: J38
- Vertices: 30
- Faces: 32
- Edges: 60
Elongated Pentagonal Gyrobicupola
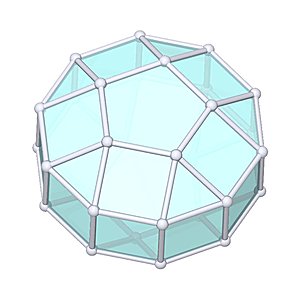  Elongated Pentagonal Gyrobicupola |
- Johnson Solid: J39
- Vertices: 30
- Faces: 32
- Edges: 60
Elongated Pentagonal Orthocupolarotunda
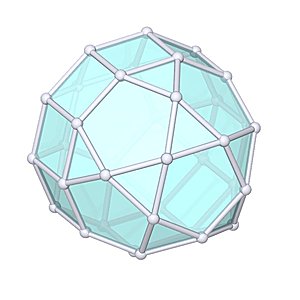  Elongated Pentagonal Orthocupolarotunda |
- Johnson Solid: J40
- Vertices: 35
- Faces: 37
- Edges: 70
Elongated Pentagonal Gyrocupolarotunda
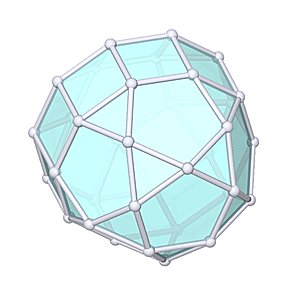  Elongated Pentagonal Gyrocupolarotunda |
- Johnson Solid: J41
- Vertices: 35
- Faces: 37
- Edges: 70
Elongated Pentagonal Orthobirotunda
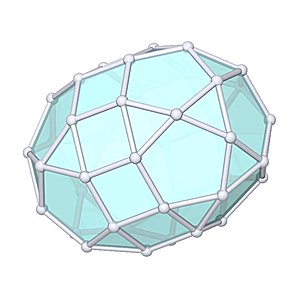  Elongated Pentagonal Orthobirotunda |
- Johnson Solid: J42
- Vertices: 40
- Faces: 42
- Edges: 80
Elongated Pentagonal Gyrobirotunda
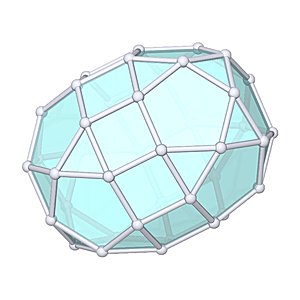  Elongated Pentagonal Gyrobirotunda |
- Johnson Solid: J43
- Vertices: 40
- Faces: 42
- Edges: 80
Gyroelongated Triangular Bicupola
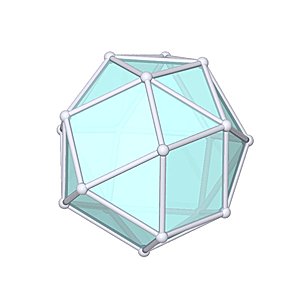  Gyroelongated Triangular Bicupola |
- Johnson Solid: J44
- Vertices: 18
- Faces: 26
- Edges: 42
Gyroelongated Square Bicupola
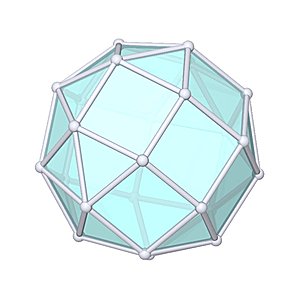  Gyroelongated Square Bicupola |
- Johnson Solid: J45
- Vertices: 24
- Faces: 34
- Edges: 56
Gyroelongated Pentagonal Bicupola
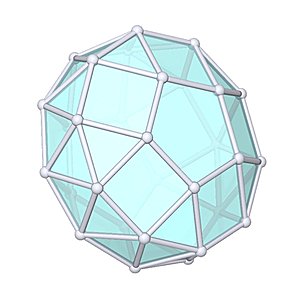  Gyroelongated Pentagonal Bicupola |
- Johnson Solid: J46
- Vertices: 30
- Faces: 42
- Edges: 70
Gyroelongated Pentagonal Cupolarotunda
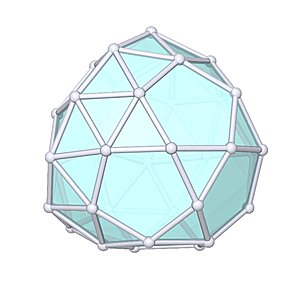  Gyroelongated Pentagonal Cupolarotunda |
- Johnson Solid: J47
- Vertices: 35
- Faces: 47
- Edges: 80
Gyroelongated Pentagonal Birotunda
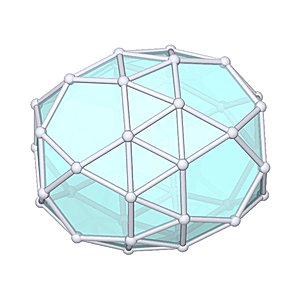  Gyroelongated Pentagonal Birotunda |
- Johnson Solid: J48
- Vertices: 40
- Faces: 52
- Edges: 90
Augmented Triangular Prism
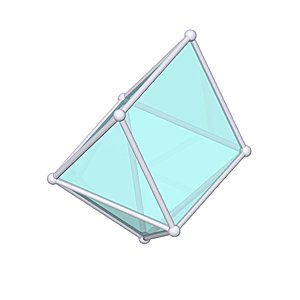  Augmented Triangular Prism |
- Johnson Solid: J49
- Vertices: 7
- Faces: 8
- Edges: 13
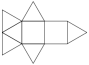
Biaugmented Triangular Prism
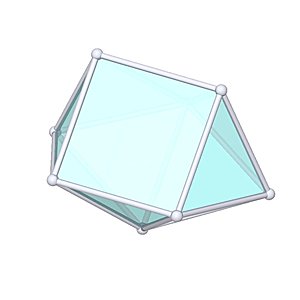  Biaugmented Triangular Prism |
- Johnson Solid: J50
- Vertices: 8
- Faces: 11
- Edges: 17
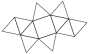
Triaugmented Triangular Prism
  Triaugmented Triangular Prism |
- Johnson Solid: J51
- Vertices: 9
- Faces: 14
- Edges: 21
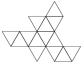
Augmented Pentagonal Prism
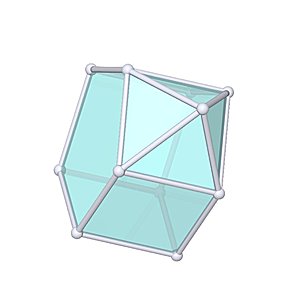  Augmented Pentagonal Prism |
- Johnson Solid: J52
- Vertices: 11
- Faces: 10
- Edges: 19
Biaugmented Pentagonal Prism
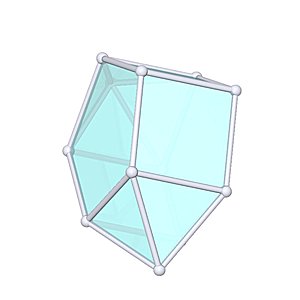  Biaugmented Pentagonal Prism |
- Johnson Solid: J53
- Vertices: 12
- Faces: 13
- Edges: 23
Augmented Hexagonal Prism
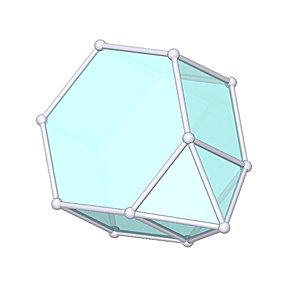  Augmented Hexagonal Prism |
- Johnson Solid: J54
- Vertices: 13
- Faces: 11
- Edges: 22
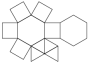
Parabiaugmented Hexagonal Prism
  Parabiaugmented Hexagonal Prism |
- Johnson Solid: J55
- Vertices: 14
- Faces: 14
- Edges: 26
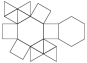
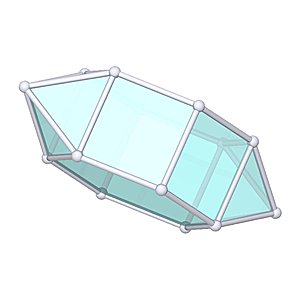
Metabiaugmented Hexagonal Prism
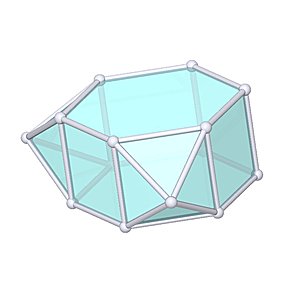  Metabiaugmented Hexagonal Prism |
- Johnson Solid: J56
- Vertices: 14
- Faces: 14
- Edges: 26
Triaugmented Hexagonal Prism
  Triaugmented Hexagonal Prism |
- Johnson Solid: J57
- Vertices: 15
- Faces: 17
- Edges: 30
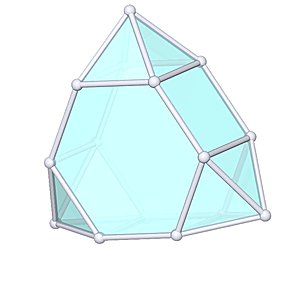
Augmented Dodecahedron
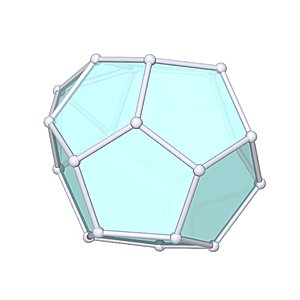  Augmented Dodecahedron |
- Johnson Solid: J58
- Vertices: 21
- Faces: 16
- Edges: 35
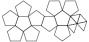
Parabiaugmented Dodecahedron
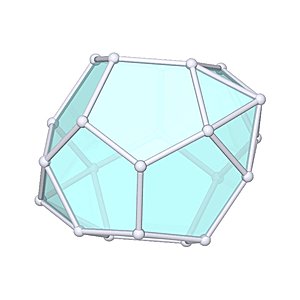  Parabiaugmented Dodecahedron |
- Johnson Solid: J59
- Vertices: 22
- Faces: 20
- Edges: 40
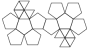
Metabiaugmented Dodecahedron
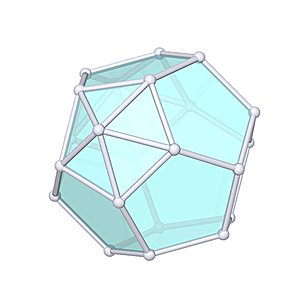  Metabiaugmented Dodecahedron |
- Johnson Solid: J60
- Vertices: 22
- Faces: 20
- Edges: 40
Triaugmented Dodecahedron
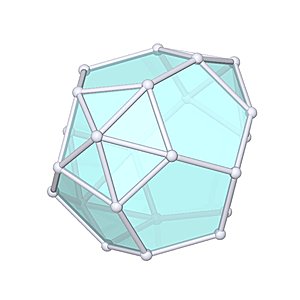  Triaugmented Dodecahedron |
- Johnson Solid: J61
- Vertices: 23
- Faces: 24
- Edges: 45
Metabidiminished Icosahedron
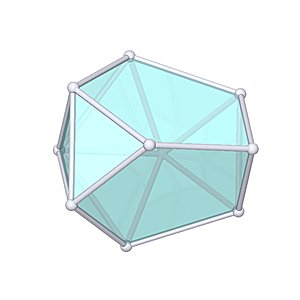  Metabidiminished Icosahedron |
- Johnson Solid: J62
- Vertices: 10
- Faces: 12
- Edges: 20
Tridiminished Icosahedron
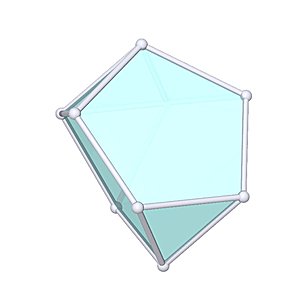  Tridiminished Icosahedron |
- Johnson Solid: J63
- Vertices: 9
- Faces: 8
- Edges: 15
Augmented Tridiminished Icosahedron
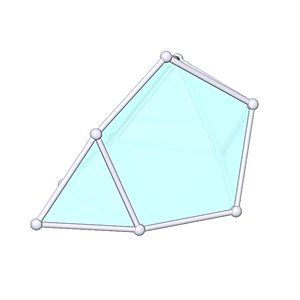  Augmented Tridiminished Icosahedron |
- Johnson Solid: J64
- Vertices: 10
- Faces: 10
- Edges: 18
Augmented Truncated Tetrahedron
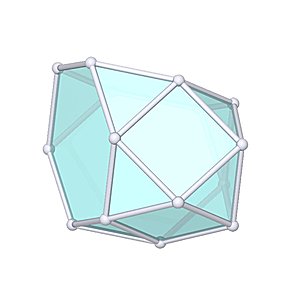  Augmented Truncated Tetrahedron |
- Johnson Solid: J65
- Vertices: 15
- Faces: 14
- Edges: 27
Augmented Truncated Cube
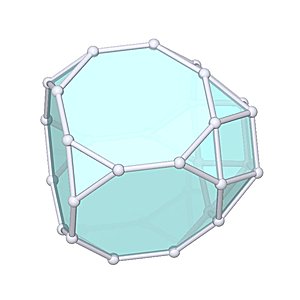  Augmented Truncated Cube |
- Johnson Solid: J66
- Vertices: 28
- Faces: 22
- Edges: 48
Biaugmented Truncated Cube
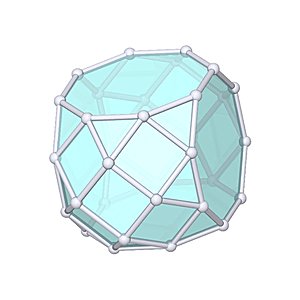  Biaugmented Truncated Cube |
- Johnson Solid: J67
- Vertices: 32
- Faces: 30
- Edges: 60
Augmented Truncated Dodecahedron
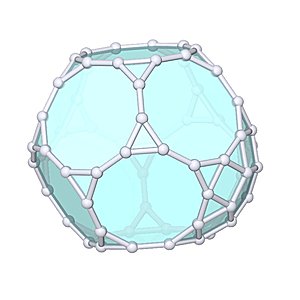  Augmented Truncated Dodecahedron |
- Johnson Solid: J68
- Vertices: 65
- Faces: 42
- Edges: 105
Parabiaugmented Truncated Dodecahedron
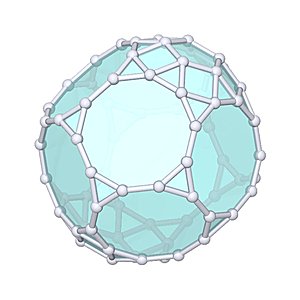  Parabiaugmented Truncated Dodecahedron |
- Johnson Solid: J69
- Vertices: 70
- Faces: 52
- Edges: 120
Metabiaugmented Truncated Dodecahedron
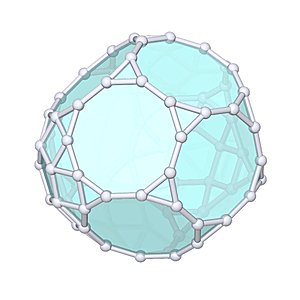  Metabiaugmented Truncated Dodecahedron |
- Johnson Solid: J70
- Vertices: 70
- Faces: 52
- Edges: 120
Triaugmented Truncated Dodecahedron
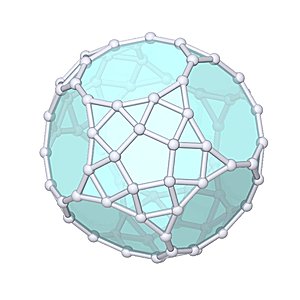  Triaugmented Truncated Dodecahedron |
- Johnson Solid: J71
- Vertices: 75
- Faces: 62
- Edges: 135
Gyrate Rhombicosidodecahedron
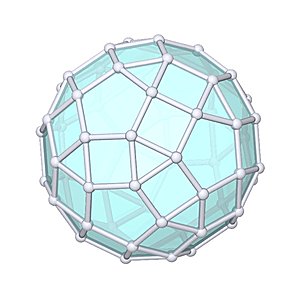  Gyrate Rhombicosidodecahedron |
- Johnson Solid: J72
- Vertices: 60
- Faces: 62
- Edges: 120
Parabigyrate Rhombicosidodecahedron
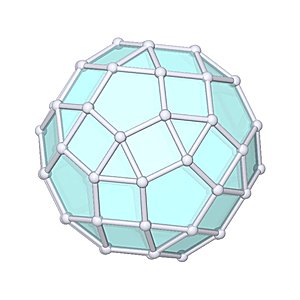  Parabigyrate Rhombicosidodecahedron |
- Johnson Solid: J73
- Vertices: 60
- Faces: 62
- Edges: 120
Metabigyrate Rhombicosidodecahedron
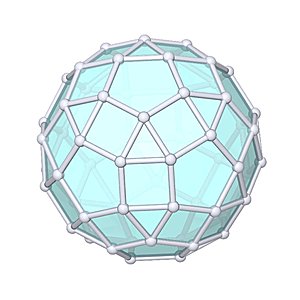  Metabigyrate Rhombicosidodecahedron |
- Johnson Solid: J74
- Vertices: 60
- Faces: 62
- Edges: 120
Trigyrate Rhombicosidodecahedron
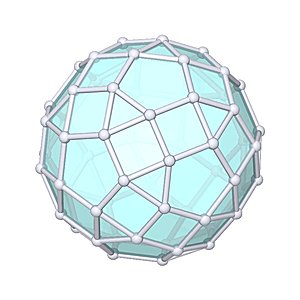  Trigyrate Rhombicosidodecahedron |
- Johnson Solid: J75
- Vertices: 60
- Faces: 62
- Edges: 120
Diminished Rhombicosidodecahedron
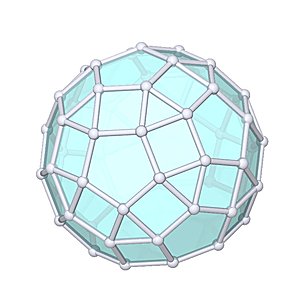  Diminished Rhombicosidodecahedron |
- Johnson Solid: J76
- Vertices: 55
- Faces: 52
- Edges: 105
Paragyrate Diminished Rhombicosidodecahedron
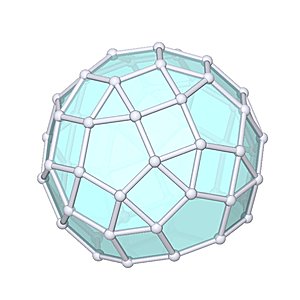  Paragyrate Diminished Rhombicosidodecahedron |
- Johnson Solid: J77
- Vertices: 55
- Faces: 52
- Edges: 105
Metagyrate Diminished Rhombicosidodecahedron
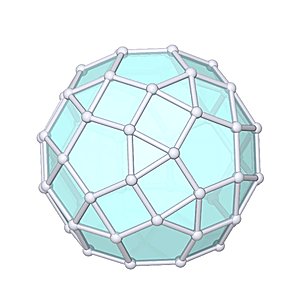  Metagyrate Diminished Rhombicosidodecahedron |
- Johnson Solid: J78
- Vertices: 55
- Faces: 52
- Edges: 105
Bigyrate Diminished Rhombicosidodecahedron
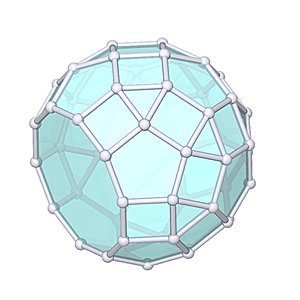  Bigyrate Diminished Rhombicosidodecahedron |
- Johnson Solid: J79
- Vertices: 55
- Faces: 52
- Edges: 105
Parabidiminished Rhombicosidodecahedron
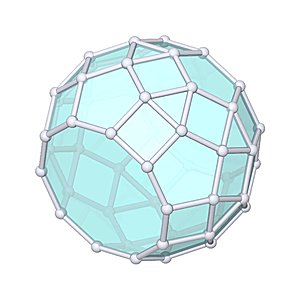  Parabidiminished Rhombicosidodecahedron |
- Johnson Solid: J80
- Vertices: 50
- Faces: 42
- Edges: 90
Metabidiminished Rhombicosidodecahedron
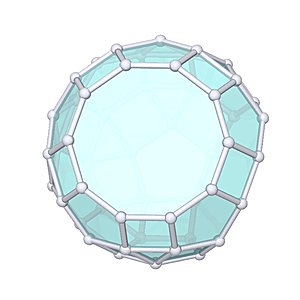  Metabidiminished Rhombicosidodecahedron |
- Johnson Solid: J81
- Vertices: 50
- Faces: 42
- Edges: 90
Gyrate Bidiminished Rhombicosidodecahedron
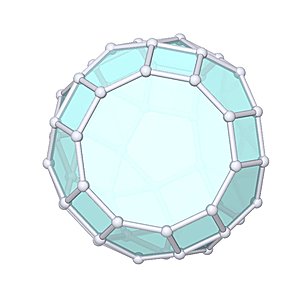  Gyrate Bidiminished Rhombicosidodecahedron |
- Johnson Solid: J82
- Vertices: 50
- Faces: 42
- Edges: 90
Tridiminished Rhombicosidodecahedron
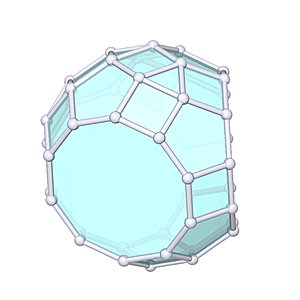  Tridiminished Rhombicosidodecahedron |
- Johnson Solid: J83
- Vertices: 45
- Faces: 32
- Edges: 75
Snub Disphenoid
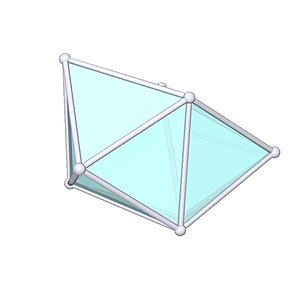  Snub Disphenoid |
- Johnson Solid: J84
- Vertices: 8
- Faces: 12
- Edges: 18
Snub Square Antiprism
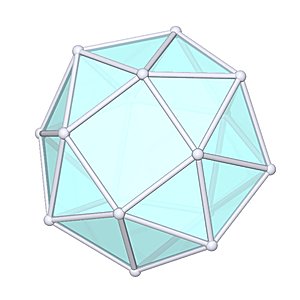  Snub Square Antiprism |
- Johnson Solid: J85
- Vertices: 16
- Faces: 26
- Edges: 40
Sphenocorona
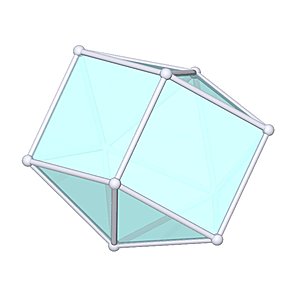  Sphenocorona |
- Johnson Solid: J86
- Vertices: 10
- Faces: 14
- Edges: 22
Augmented Sphenocorona
  Augmented Sphenocorona |
- Johnson Solid: J87
- Vertices: 11
- Faces: 17
- Edges: 26
Sphenomegacorona
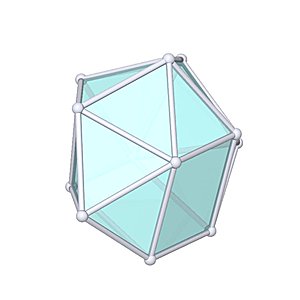  Sphenomegacorona |
- Johnson Solid: J88
- Vertices: 12
- Faces: 18
- Edges: 28
Hebesphenomegacorona
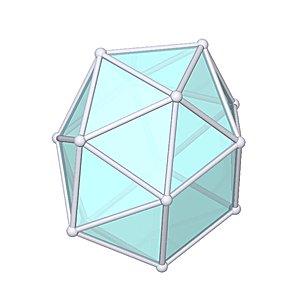  Hebesphenomegacorona |
- Johnson Solid: J89
- Vertices: 14
- Faces: 21
- Edges: 33
Disphenocingulum
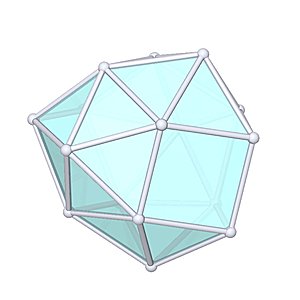  Disphenocingulum |
- Johnson Solid: J90
- Vertices: 16
- Faces: 24
- Edges: 38
Bilunabirotunda
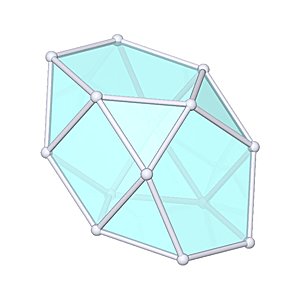  Bilunabirotunda |
- Johnson Solid: J91
- Vertices: 14
- Faces: 14
- Edges: 26
Triangular Hebesphenorotunda
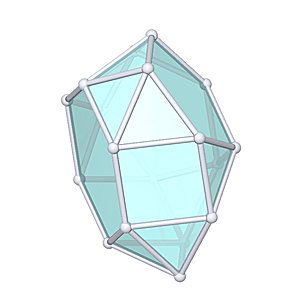  Triangular Hebesphenorotunda |
- Johnson Solid: J92
- Vertices: 18
- Faces: 20
- Edges: 36
References
- Johnson Solid
 , Mathworld
, Mathworld
- Johnson Solid
 , Wikipedia
, Wikipedia
- George Hart
 , very interesting web-site, also from where I've got the wrl-files and converted into .pov to render the models
, very interesting web-site, also from where I've got the wrl-files and converted into .pov to render the models
Uniform Polyhedra
For sake of completeness I list all "uniform polyhedra", which include the platonic and archimedean solids but additionally cover als the concave (non-convex) polyhedra which aren't suitable for habitat development.
References
- Uniform Polyhedron
 , Mathworld
, Mathworld
- Uniform Polyhedron
 , Wikipedia
, Wikipedia
- List of Uniform Polyhedra
 , Wikipedia
, Wikipedia
Waterman Polyhedra
Waterman polyhedra exist in mathematics since about 1990, a rather recent discovery. The concept of Waterman polyhedra was developed by Steve Waterman and relate to "Cubic Close Packing" (CCP) of spheres,
also known as IVM (Isotropic Vector Matrix) by R. Buckminster Fuller.
and relate to "Cubic Close Packing" (CCP) of spheres,
also known as IVM (Isotropic Vector Matrix) by R. Buckminster Fuller.
Spheres are packed in a cubic manner:
- x, y and z are integers,
- sphere diameter is √2 thereby,
- at 0,0,0 resides the first sphere,
and then those removed which have longer vector than √(2*n) from the center (0,0,0) and then a convex hull is calculated which gives a polyhedron:
|
|
Some More Examples
Different Origins
Several origins are available as summarized by Mirek Majewski  :
:
| Origin | Origin Location | radius | Comment |
| 1 | 0,0,0 | √(2*n) | Atom center: traditional origin of Waterman polyhedra, symmetry properties of a cube. |
| 2 | 1/2,1/2,0 | √(2+4*n)/2 | Touch point between 2 atoms: symmetry properties of flat rectangle whose top & bottom faces are the same |
| 3 | 1/3,1/3,2/3 | √(6*(n+1))/3 | Void center between 3 atoms: symmetry properties of flat triangle whose top & bottom faces are different |
| 3* | 1/3,1/3,1/3 | √(3+6*n)/3 | Void center between 3 lattice voids: same symmetry of origin 3. |
| 4 | 1/2,1/2,1/2 | √(3+8*(n-1))/2 | Tretrahedron void center between 4 atoms: symmetry properties of a tetrahedron. |
| 5 | 0,0,1/2 | √(1+4*n)/2 | 5 atoms: symmetry properties of a flat rectangle whose top & bottom are different. |
| 6 | 1,0,0 | √(1+2*(n-1)) | Octahedral void center between 6 atoms: symmetry properties of a cube. |
7 Origins of Waterman Polyhedra by Mark Newbold  |
|||
whereas n starts with 1 for all origins.
| O1 | O2 | O3 | O3* | O4 | O5 | O6 | |
| W1 |  |  |  |  |  |  |  |
| W2 |  |  |  |  |  |  |  |
| W3 | 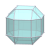 |  |  |  |  |  |  |
| W4 |  |  |  |  |  |  |  |
| W5 |  | 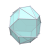 |  | 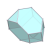 |  |  |  |
| W6 |  |  |  |  |  |  |  |
| W7 |  |  |  |  |  |  |  |
| W8 |  |  |  |  |  | 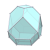 | 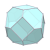 |
| W9 |  | 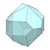 | 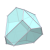 | 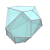 |  | 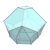 |  |
| W10 |  |  |  | 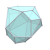 |  |  |  |
Features of Waterman Polyhedra
So the nice thing is, the creation of the polyhedra is done parametrically, in other words, systematically. Needless to say, there are infinite of Waterman polyhedra, and interestingly there are doubles to be encountered, where:
- the same amount of packed spheres result in the same polyhedra (14 + 16 n) m2 (whereas n & m integers >= 0)
- the final polyhedra from packed spheres result in a previous discovered polyhedra when normalized (e.g. W3 O1 = W24 O1)
Those are not yet removed in the overview which follows.
Platonic & Archimedean Solids vs Waterman Polyhedra
The Waterman Polyhedra (WP) covers also some of the platonic and archimedean solids. For sake of this comparison the WP are normalized, as W2 O1 has a different size/volume than W1 O6, but the same form of a Octahedron.Platonic Solids
|
|
|
|||
| W1 O3* = W2 O3* = W1 O3 = W1 O4 = Tretrahedron | W2 O1 = W1 O6 = Octahedron | W2 O6 = Cube |
Icosahedron and Dodecahedron have no WP representation.
Archimedean Solids
|
|
|
|||
| W1 O1 = W4 O1 = Cuboctahedron | W10 O1 = Truncated Octahedron | W4 O3 = W2 O4 = Truncated Tetrahedron |
The following look like archimedean solids, but they are not:
|
|
||
| W7 O1 != Truncated Cuboctahedron | W3 O1 = W12 O1 != Rhombicuboctahedron |
as they are not having one length of edge, but two lengths of edges.
The others have no WP representation.
The Generalized Waterman Polyhedra (GWP) are currently still sorted by Steve Waterman, and I will include them later as they may cover more platonic and archimedean solids.
References
- Waterman Polyhedron
 , very informative site by Steve Waterman, the inventor of the Waterman polyhedra
, very informative site by Steve Waterman, the inventor of the Waterman polyhedra
- Paul Bourke
 has also a comprehensive website (I highly recommend to visit), his waterman.c
has also a comprehensive website (I highly recommend to visit), his waterman.c  I used to calculate those rendered Waterman polyhedra.
I used to calculate those rendered Waterman polyhedra.
- 3D Junkyard
 , vast & interesting collection of links by David Eppstein
, vast & interesting collection of links by David Eppstein